��Ŀ����
13����֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������Ϊe=$\frac{1}{2}$���ҹ��㣨$\frac{1}{3}$��$\frac{\sqrt{13}}{2}$����1������ԲC�ķ��̣�
��2����֪A��B����Բ�ϵ����㣬��M������Ϊ��1��0������A��B���㲻����x��Գ�ʱ����̽���MAB�ܷ�Ϊ�ȱ������Σ���˵�����ɣ�
���� ��1������ԲC��������Ϊe=$\frac{1}{2}$���ҹ��㣨$\frac{1}{3}$��$\frac{\sqrt{13}}{2}$�����ɵ�$\left\{\begin{array}{l}{\frac{c}{a}=\frac{1}{2}}\\{{a}^{2}={b}^{2}+{c}^{2}}\\{\frac{1}{9{a}^{2}}+\frac{13}{4{b}^{2}}=1}\end{array}\right.$����ü��ɣ�
��2������i����AB��x��ʱ������Բ���������ɵ�������MABΪ�ȱ������Σ�
��ii����AB��x�ƽ��Ҳ����ֱʱ����ֱ��AB�ķ���Ϊy=kx+m����A��x1��y1����B��x2��y2�����߶�AB���е�N��x0��y0����ֱ�߷�������Բ���������ɵã���9+12k2��x2+24kmx+12m2-40=0���ɡ���0���õ�9m2��30+40k2�����ø���ϵ���Ĺ�ϵ�ɵã�N$��\frac{-12km}{9+12{k}^{2}}��\frac{9m}{9+12{k}^{2}}��$����M��0��1��������MABΪ�ȱ������Σ���kMN•k=-1����Ϊm=-3-4k2���������0����Ϊ144k4+176k2+51��0�����˷����Ƿ��н⼴�ɣ�
��� �⣺��1������ԲC��������Ϊe=$\frac{1}{2}$���ҹ��㣨$\frac{1}{3}$��$\frac{\sqrt{13}}{2}$����
��$\left\{\begin{array}{l}{\frac{c}{a}=\frac{1}{2}}\\{{a}^{2}={b}^{2}+{c}^{2}}\\{\frac{1}{9{a}^{2}}+\frac{13}{4{b}^{2}}=1}\end{array}\right.$�����b2=$\frac{10}{3}$��a2=$\frac{40}{9}$��
����ԲC�ķ���Ϊ��$\frac{9{x}^{2}}{40}+\frac{3{y}^{2}}{10}=1$��
��2����i����AB��x��ʱ��ֱ��AM��б��Ϊ$\sqrt{3}$������Ϊy=$\sqrt{3}$x+1������Բ���������ɵ�������MABΪ�ȱ������Σ�
��ii����AB��x�ƽ��Ҳ����ֱʱ����ֱ��AB�ķ���Ϊy=kx+m��
��A��x1��y1����B��x2��y2�����߶�AB���е�N��x0��y0����
����$\left\{\begin{array}{l}{\frac{9{x}^{2}}{40}+\frac{3{y}^{2}}{10}=1}\\{y=kx+m}\end{array}\right.$����ȥy�ɵã���9+12k2��x2+24kmx+12m2-40=0���ɡ���0���õ�9m2��30+40k2��
��x1+x2=$\frac{-24km}{9+12{k}^{2}}$��y1+y2=k��x1+x2��+2m=$\frac{18m}{9+12{k}^{2}}$��
���N$��\frac{-12km}{9+12{k}^{2}}��\frac{9m}{9+12{k}^{2}}��$����M��0��1����
����MABΪ�ȱ������Σ���kMN•k=-1��
��$\frac{\frac{9m}{9+12{k}^{2}}-1}{\frac{-12km}{9+12{k}^{2}}-0}$��k=-1����Ϊm=-3-4k2��
�������0����Ϊ144k4+176k2+51��0��
����${k}_{1}^{2}+{k}_{2}^{2}$=-$\frac{176}{144}$������⣮
���Ͽɵã�ֻ�е�AB��x��ʱ������Բ���������ɵ�������MABΪ�ȱ������Σ�
���� ���⿼������Բ�ı����̼������ʡ�ֱ������Բ�ཻ����ת��Ϊ���������ɵá���0�������ϵ���Ĺ�ϵ���ȱ������ε����ʣ���������������������������������⣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�| A�� | $\frac{29}{2}$ | B�� | $\frac{21}{2}$ | C�� | -$\frac{11}{2}$ | D�� | $\frac{11}{2}$ |
| A�� | y=x-1 | B�� | y=ln��x+1�� | C�� | y=��$\frac{1}{2}$��x | D�� | y=x+$\frac{1}{x}$ |
| A�� | 21 | B�� | 19 | C�� | 31 | D�� | 29 |
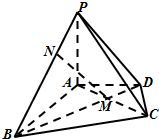 ������P-ABCD�У�PA��ƽ��ABCD����ABC���������Σ�AC��BD�Ľ���Mǡ����AC�е㣬��PA=AB=4����CDA=120�㣬��N���߶�PB�ϣ���PN=$\sqrt{2}$��
������P-ABCD�У�PA��ƽ��ABCD����ABC���������Σ�AC��BD�Ľ���Mǡ����AC�е㣬��PA=AB=4����CDA=120�㣬��N���߶�PB�ϣ���PN=$\sqrt{2}$��