题目内容
【题目】(本小题满分为14分)已知定义域为R的函数![]() 是奇函数.
是奇函数.
(1)求a,b的值;
(2)若对任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的取值范围.
【答案】(1)a=2,b=1.(2)![]()
【解析】
试题分析:(1)利用奇函数性质列出两个独立条件解出a,b的值,注意要验证. 因为定义域为R,所以有f(0)=0,从而b=1.再取f(1)=-f(-1)得a=2,代入函数验证![]() (2)利用函数奇偶性及单调性化简不等式:因f(x)是奇函数,从而不等式f(t2-2t)+f(2t2-k)<0等价于f(t2-2t)<-f(2t2-k)=f(-2t2+k). 因为f(x)是减函数,其又等价于t2-2t>-2t2+k.对一切t∈R恒成立,即Δ=4+12k<0,解得
(2)利用函数奇偶性及单调性化简不等式:因f(x)是奇函数,从而不等式f(t2-2t)+f(2t2-k)<0等价于f(t2-2t)<-f(2t2-k)=f(-2t2+k). 因为f(x)是减函数,其又等价于t2-2t>-2t2+k.对一切t∈R恒成立,即Δ=4+12k<0,解得![]()
试题解析: (1)因为f(x)是奇函数,且定义域为R,所以f(0)=0,
即![]() =0,解得b=1.
=0,解得b=1.
从而有![]() .又由f(1)=-f(-1)知
.又由f(1)=-f(-1)知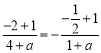 ,解得a=2----6分
,解得a=2----6分
经检验适合题意,∴a=2,b=1.
(2)由(1)知![]()
由上式易知f(x)在(-∞,+∞)上为减函数.又因f(x)是奇函数,
从而不等式f(t2-2t)+f(2t2-k)<0等价于f(t2-2t)<-f(2t2-k)=f(-2t2+k).-----10分
因为f(x)是减函数,由上式推得t2-2t>-2t2+k.
即对一切t∈R有3t2-2t-k>0.
从而判别式Δ=4+12k<0,解得![]()

【题目】某制造厂商10月份生产了一批乒乓球,从中随机抽取n个进行检查,测得每个球的直径(单位:mm),将数据进行分组,得到如表频率分布表:
分组 | 频数 | 频率 |
[39.95,39.97) | 6 | P1 |
[39.97,39.99) | 12 | 0.20 |
[39.99,40.01) | a | 0.50 |
[40.01,40.03) | b | P2 |
合计 | n | 1.00 |
(1)求a、b、n及P1、P2的值,并画出频率分布直方图(结果保留两位小数); 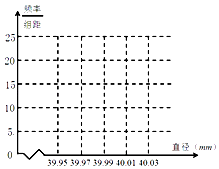
(2)已知标准乒乓球的直径为40.00mm,直径误差不超过0.01mm的为五星乒乓球,若这批乒乓球共有10000个,试估计其中五星乒乓球的数目;
(3)统计方法中,同一组数据常用该组区间的中点值(例如区间[39.99,40.01)的中点值是40.00)作为代表,估计这批乒乓球直径的平均值和中位数.