题目内容
【题目】设数列{an}的前n项和为Sn ， 且Sn=n2﹣4n﹣5．
（1）求数列{an}的通项公式；
（2）设bn=|an|，数列{bn}的前n项和为Tn ， 求Tn ．
【答案】
（1）解：∵Sn=n2﹣4n﹣5，
∴当n≥2时，an=Sn﹣Sn﹣1=n2﹣4n﹣5﹣[（n﹣1）2﹣4（n﹣1）﹣5]=2n﹣5，
又当n=1时，a1=﹣8不适合上式，
∴an= 
（2）解：∵bn=|an|，数列{bn}的前n项和为Tn，
当n=1时，b1=|a1|=8，T1=8；
当n=2时，b2=|a2|=1，T2=8+1=9；
∵n≥3时，an=2n﹣5≥1＞0，
∴bn=|an|=an=2n﹣5，
∴Tn=8+1+（1+3+…+2n﹣5）=9+ 
=（n﹣2）2+9=n2﹣4n+13．
综上，Tn=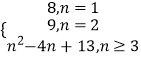 
【解析】（1）由Sn=n2﹣4n﹣5，可得当n≥2时，an=Sn﹣Sn﹣1=2n﹣5，再检验当n=1时，a1是否适合上式，即可求得数列{an}的通项公式；（2）由bn=|an|=|2n﹣5|，分n=1、n=2、n≥3三类讨论，分别求得数列{bn}的前n项和Tn ， 最后综合起来即可求．
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识，掌握数列{an}的前n项和sn与通项an的关系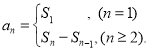
，以及对数列的通项公式的理解，了解如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式．
练习册系列答案
相关题目
