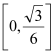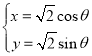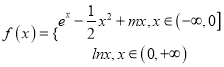题目内容
【题目】在某校举行的航天知识竞赛中,参与竞赛的文科生与理科生人数之比为![]() ,且成绩分布在
,且成绩分布在![]() ,分数在
,分数在![]() 以上(含
以上(含![]() )的同学获奖. 按文理科用分层抽样的方法抽取
)的同学获奖. 按文理科用分层抽样的方法抽取![]() 人的成绩作为样本,得到成绩的频率分布直方图(见下图).
人的成绩作为样本,得到成绩的频率分布直方图(见下图).
(1)填写下面的![]() 列联表,能否有超过
列联表,能否有超过![]() 的把握认为“获奖与学生的文理科有关”?
的把握认为“获奖与学生的文理科有关”?
(2)将上述调査所得的频率视为概率,现从参赛学生中,任意抽取![]() 名学生,记“获奖”学生人数为
名学生,记“获奖”学生人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
文科生 | 理科生 | 合计 | |
获奖 |
| ||
不获奖 | |||
合计 |
|
附表及公式:
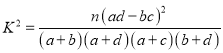 ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
【答案】(1)表见解析,有把握;(2)分布列见解析,![]() .
.
【解析】
试题分析:(1)首先根据频率分布直方图完成表格数据,然后根据公式计算出![]() ,再与临界表比较,从而作出结论;(2)首先求得
,再与临界表比较,从而作出结论;(2)首先求得![]() 的所有可能取值,然后分别求出相应概率,由此列出分布列,求得数学期望.
的所有可能取值,然后分别求出相应概率,由此列出分布列,求得数学期望.
试题解析:(1)
文科生 | 理科生 | 合计 | |
获奖 | 5 | 35 | 40 |
不获奖 | 45 | 115 | 160 |
合计 | 50 | 150 | 200 |
k==≈4.167>3.841,
所以有超过95%的把握认为“获奖与学生的文理科有关”. …6分
(2)由表中数据可知,抽到获奖同学的概率为,
将频率视为概率,所以X可取0,1,2,3,且X~B(3,).
P(X=k)=C×()k(1-)3-k(k=0,1,2,3),
X | 0 | 1 | 2 | 3 |
P |
…10分
E(X)=3×=. …12分

 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案【题目】近年来我国电子商务行业迎来蓬勃发展的新机遇,2016年双11期间,某平台的销售业绩高达918亿人民币,与此同时,相关管理部门也推出了针对电商的商品和服务评价体系,现从评价系统中随机选出200次成功的交易,并对其评价结果进行统计,对商品的好评率为![]() ,对服务的好评率为
,对服务的好评率为![]() ,其中对商品和服务都做出好评的交易为80次.
,其中对商品和服务都做出好评的交易为80次.
在犯错误概率不超过( )的前提下,认为商品好评与服务好评有关.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()