题目内容
【题目】在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,∠CDA=∠BAD=90°,AB=AD=2DC=2 ![]() ,PA=4且E为PB的中点.
,PA=4且E为PB的中点. 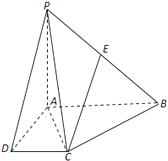
(1)求证:CE∥平面PAD;
(2)求直线CE与平面PAC所成角的正弦值.
【答案】
(1)证明:取PA中点Q,连结QE、QD,
∵E为PB中点,∴QE∥AB,且QE= ![]() AB,
AB,
∵底面ABCD是直角梯形,∠CDA=∠BDA=90°,AB=AD=2DC=2 ![]() ,
,
∴QE∥CD,且QE=CD,∴四边形QECD是平行四边形,
∴EC∥QD,又FC平面PAD,QD平面PAD,
∴CE∥平面PAD
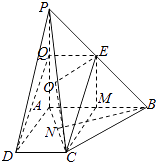
(2)解:过E作平面PAC的垂线,记垂足为O,连结CO,
则∠ECO是直线CE与平面PAC所成的角,
过B作BN⊥AC,记垂足为N,
∵PA⊥平面ABCD,∴PA⊥BN,
又PA,AC平面PAC,且PA∩AC=A,
∴BN⊥平面PAC,
∴EO∥BN,又∵E是AB的中点,∴EO= ![]() BN=
BN= ![]() ,
,
过E作EM⊥AB=M,连结CM,得CE=2 ![]() ,
,
在Rt△CEO中,sin∠ECO= ![]() =
= ![]() ,
,
∴直线CE与平面PAC所成角的正弦值为 ![]() .
.
【解析】(1)取PA中点Q,连结QE、QD,推导出四边形QECD是平行四边形,由此能证明CE∥平面PAD.(2)过E作平面PAC的垂线,记垂足为O,连结CO,∠ECO是直线CE与平面PAC所成的角,过B作BN⊥AC,记垂足为N,过E作EM⊥AB=M,连结CM,由此能求出直线CE与平面PAC所成角的正弦值.
【考点精析】利用直线与平面平行的判定和空间角的异面直线所成的角对题目进行判断即可得到答案,需要熟知平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则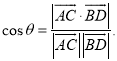 .
.

【题目】某研究小组为了研究某品牌智能手机在正常使用情况下的电池供电时间,分别从该品牌手机的甲、乙两种型号中各选取![]() 部进行测试,其结果如下:
部进行测试,其结果如下:
甲种手机供电时间(小时) |
|
|
|
|
|
|
乙种手机供电时间(小时) |
|
|
|
|
|
|
(1)求甲、乙两种手机供电时间的平均值与方差,并判断哪种手机电池质量好;
(2)为了进一步研究乙种手机的电池性能,从上述![]() 部乙种手机中随机抽取
部乙种手机中随机抽取![]() 部,记所抽
部,记所抽![]() 部手机供电时间不小于
部手机供电时间不小于![]() 小时的个数为
小时的个数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.