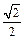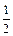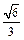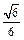题目内容
(12分)已知焦点在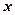 轴上,离心率为
轴上,离心率为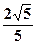 的椭圆的一个顶点是抛物线
的椭圆的一个顶点是抛物线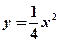 的焦点,过椭圆右焦点
的焦点,过椭圆右焦点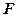 的直线
的直线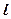 交椭圆于
交椭圆于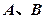 两点,交
两点,交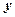 轴于点
轴于点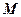 ,且
,且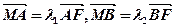 ,(1)求椭圆方程;(2)证明:
,(1)求椭圆方程;(2)证明: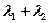 为定值
为定值
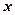 轴上,离心率为
轴上,离心率为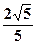 的椭圆的一个顶点是抛物线
的椭圆的一个顶点是抛物线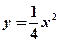 的焦点,过椭圆右焦点
的焦点,过椭圆右焦点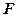 的直线
的直线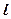 交椭圆于
交椭圆于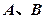 两点,交
两点,交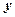 轴于点
轴于点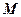 ,且
,且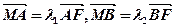 ,(1)求椭圆方程;(2)证明:
,(1)求椭圆方程;(2)证明: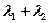 为定值
为定值(1)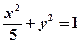
(2)证明见解析。
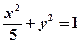
(2)证明见解析。
(1)由题意知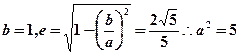
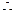 椭圆的方程为
椭圆的方程为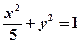 (5分)
(5分)
(2)设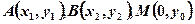 ,由
,由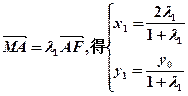
由 ,又
,又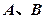 在椭圆上代入椭圆方程知
在椭圆上代入椭圆方程知
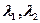 是方程
是方程 两根,所以
两根,所以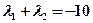 (定值)(12分)
(定值)(12分)
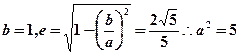
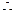 椭圆的方程为
椭圆的方程为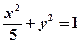 (5分)
(5分)(2)设
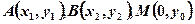 ,由
,由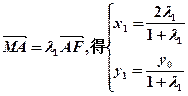
由
 ,又
,又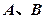 在椭圆上代入椭圆方程知
在椭圆上代入椭圆方程知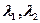 是方程
是方程 两根,所以
两根,所以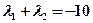 (定值)(12分)
(定值)(12分)
练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
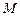 过定点
过定点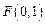 ,且和定直线
,且和定直线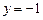 相切.(Ⅰ)求动圆圆心
相切.(Ⅰ)求动圆圆心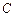 的方程;(Ⅱ)已知点
的方程;(Ⅱ)已知点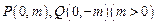 ,过点
,过点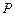 作直线与曲线
作直线与曲线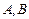 两点,若
两点,若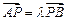 (
(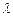
 为实数),证明:
为实数),证明: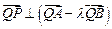 .
.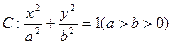 ,通径长为1,且焦点与短轴两端点构成等边三角形,(1)求椭圆的方程;(2)过点Q(-1,0)的直线l交椭圆于A,B两点,交直线x=-4于点E,点Q分
,通径长为1,且焦点与短轴两端点构成等边三角形,(1)求椭圆的方程;(2)过点Q(-1,0)的直线l交椭圆于A,B两点,交直线x=-4于点E,点Q分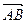 所成比为λ,点E分
所成比为λ,点E分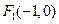 出发,经直线l:
出发,经直线l: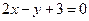 上一点
上一点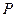 反射后,恰好穿过点
反射后,恰好穿过点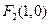 .(1)求
.(1)求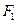 、
、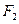 为焦点且过点
为焦点且过点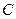 的方程; (3)设点
的方程; (3)设点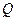 是椭圆
是椭圆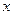 轴上是否存在两定点
轴上是否存在两定点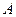 、
、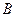 ,使得直线
,使得直线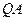 、
、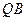 的斜率之积为定值?若存在,请求出定值,并求出所有满足条件的定点
的斜率之积为定值?若存在,请求出定值,并求出所有满足条件的定点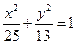 的焦点为焦点,以抛物线
的焦点为焦点,以抛物线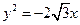 的准线为右准线.
的准线为右准线.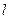 :
: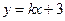 与双曲线M相交于A、B两点,O是原点.
与双曲线M相交于A、B两点,O是原点.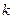 为何值时,使得
为何值时,使得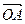
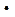
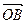
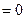 ?
?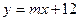 对称?若存在,求出
对称?若存在,求出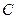 :
: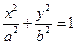
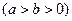 的两个焦点为
的两个焦点为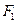 、
、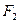 ,点
,点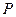 在椭圆
在椭圆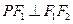 ,
,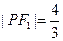 ,
,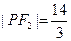 .
.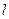 过圆
过圆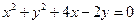 的圆心
的圆心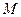 ,交椭圆
,交椭圆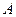 、
、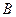 两点,且
两点,且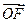 所在直线为
所在直线为 轴,建立如 所示的坐标系。设
轴,建立如 所示的坐标系。设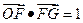 ,点F的坐标为
,点F的坐标为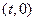 ,
,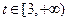 ,点G的坐标为
,点G的坐标为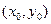 。
。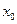 关于
关于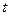 的函数
的函数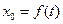 的表达式,判断函数
的表达式,判断函数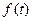 的单调性,并证明你的判断;
的单调性,并证明你的判断;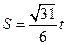 ,若以O为中心,F为焦点的椭圆经过点G,求当
,若以O为中心,F为焦点的椭圆经过点G,求当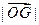 取最小值时椭圆的方程;
取最小值时椭圆的方程;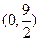 ,C、D是椭圆上的两点,且
,C、D是椭圆上的两点,且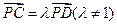 ,求实数
,求实数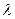 的取值范围。
的取值范围。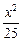 +
+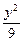 =1上一点P到左焦点F1的距离为2,M是线段PF1的中点,则M到原点O的距离等于
=1上一点P到左焦点F1的距离为2,M是线段PF1的中点,则M到原点O的距离等于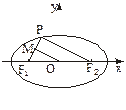
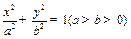 与双曲线
与双曲线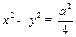 有相同的焦点,则椭圆的离心率为
有相同的焦点,则椭圆的离心率为