题目内容
椭圆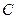 :
: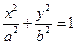
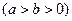 的两个焦点为
的两个焦点为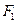 、
、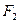 ,点
,点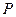 在椭圆
在椭圆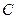 上,且
上,且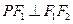 ,
,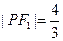 ,
,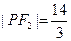 .
.
(Ⅰ)求椭圆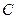 的方程;
的方程;
(Ⅱ)若直线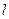 过圆
过圆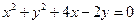 的圆心
的圆心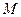 ,交椭圆
,交椭圆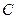 于
于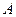 、
、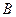 两点,且
两点,且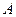 、
、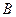 关于点
关于点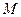 对称,求直线
对称,求直线 的方程.
的方程.
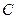 :
: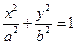
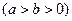 的两个焦点为
的两个焦点为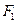 、
、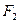 ,点
,点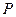 在椭圆
在椭圆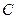 上,且
上,且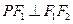 ,
,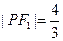 ,
,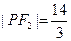 .
.(Ⅰ)求椭圆
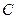 的方程;
的方程;(Ⅱ)若直线
 过圆
过圆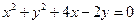 的圆心
的圆心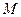 ,交椭圆
,交椭圆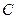 于
于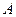 、
、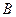 两点,且
两点,且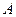 、
、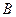 关于点
关于点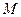 对称,求直线
对称,求直线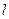 的方程.
的方程. (1)椭圆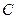 的方程为
的方程为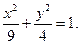 ;(2)直线
;(2)直线 的方程:
的方程: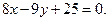
 的方程为
的方程为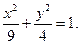 ;(2)直线
;(2)直线 的方程:
的方程: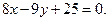
(Ⅰ)因为点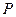 在椭圆
在椭圆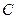 上,
上,
所以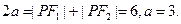
在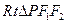 中,
中,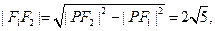
故椭圆的半焦距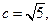 从而
从而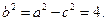
所以椭圆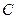 的方程为
的方程为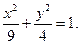
(Ⅱ)设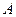 、
、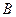 的坐标分别为
的坐标分别为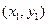 ,
,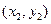 .
.
已知圆的方程为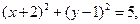
所以圆心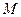 的坐标为
的坐标为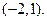
从而可设直线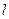 的方程为
的方程为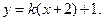
代入椭圆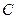 的方程得
的方程得
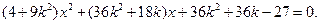
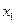 ,
,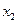 是方程的两个根,
是方程的两个根,
因为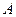 、
、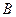 关于点
关于点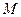 对称,
对称,
所以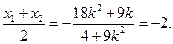 解得
解得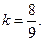
所以直线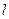 的方程
的方程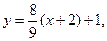
即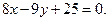
经检验,所求直线方程符合题意
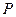 在椭圆
在椭圆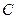 上,
上,所以
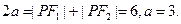
在
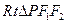 中,
中,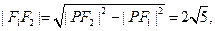
故椭圆的半焦距
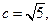 从而
从而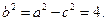
所以椭圆
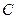 的方程为
的方程为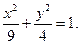
(Ⅱ)设
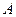 、
、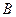 的坐标分别为
的坐标分别为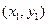 ,
,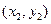 .
.已知圆的方程为
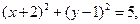
所以圆心
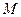 的坐标为
的坐标为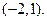
从而可设直线
 的方程为
的方程为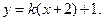
代入椭圆
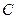 的方程得
的方程得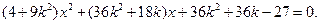
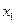 ,
,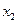 是方程的两个根,
是方程的两个根,因为
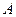 、
、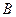 关于点
关于点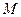 对称,
对称,所以
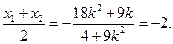 解得
解得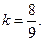
所以直线
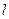 的方程
的方程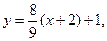
即
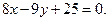
经检验,所求直线方程符合题意

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
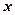 轴上,离心率为
轴上,离心率为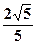 的椭圆的一个顶点是抛物线
的椭圆的一个顶点是抛物线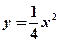 的焦点,过椭圆右焦点
的焦点,过椭圆右焦点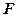 的直线
的直线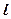 交椭圆于
交椭圆于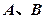 两点,交
两点,交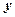 轴于点
轴于点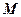 ,且
,且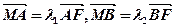 ,(1)求椭圆方程;(2)证明:
,(1)求椭圆方程;(2)证明: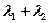 为定值
为定值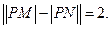
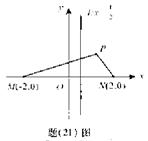
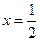 的距离,若
的距离,若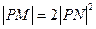 ,求
,求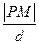 的值.
的值.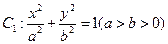 的左、右焦点分别为
的左、右焦点分别为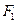 、
、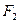 ,其中
,其中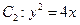 的焦点,
的焦点,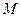 是
是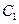 与
与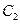 在第一象限的交点,且
在第一象限的交点,且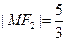 .(Ⅰ)求椭圆
.(Ⅰ)求椭圆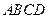 的顶点A﹑C在椭圆
的顶点A﹑C在椭圆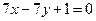 上,求直线
上,求直线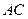 的方程.
的方程.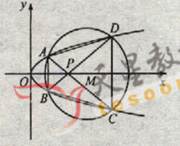 (22) (本小题满分12分)(注意:在试题卷上作答无效)如图,已知抛物线
(22) (本小题满分12分)(注意:在试题卷上作答无效)如图,已知抛物线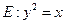
 与圆
与圆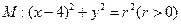 相交于A、B、C、D四个点。
相交于A、B、C、D四个点。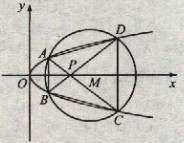
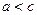 。
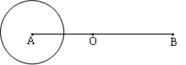
。
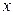 轴上,离心率
轴上,离心率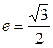 ,已知点
,已知点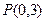 到这个椭圆上的点的最远距离是4,求这个椭圆的方程.
到这个椭圆上的点的最远距离是4,求这个椭圆的方程.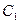 :
: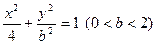 的离心率等于
的离心率等于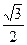 ,抛物线
,抛物线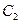 :
: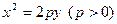 的焦点在椭圆的顶点上。(Ⅰ)求抛物线
的焦点在椭圆的顶点上。(Ⅰ)求抛物线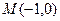 的直线
的直线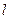 与抛物线
与抛物线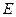 、
、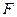 两点,又过
两点,又过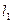 、
、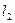 ,当
,当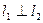 时,求直线
时,求直线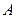 的坐标是
的坐标是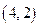 ,底边一个端点
,底边一个端点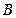 的坐标是
的坐标是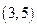 ,求另一个端点
,求另一个端点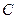 的轨迹方程,并说明它是什么图形.
的轨迹方程,并说明它是什么图形.