题目内容
(本小题满分14分)已知动圆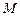 过定点
过定点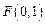 ,且和定直线
,且和定直线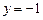 相切.(Ⅰ)求动圆圆心
相切.(Ⅰ)求动圆圆心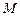 的轨迹
的轨迹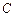 的方程;(Ⅱ)已知点
的方程;(Ⅱ)已知点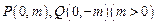 ,过点
,过点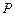 作直线与曲线
作直线与曲线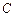 交于
交于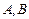 两点,若
两点,若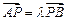 (
(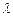
 为实数),证明:
为实数),证明: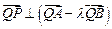 .
.
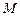 过定点
过定点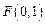 ,且和定直线
,且和定直线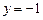 相切.(Ⅰ)求动圆圆心
相切.(Ⅰ)求动圆圆心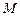 的轨迹
的轨迹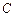 的方程;(Ⅱ)已知点
的方程;(Ⅱ)已知点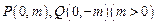 ,过点
,过点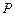 作直线与曲线
作直线与曲线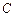 交于
交于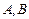 两点,若
两点,若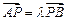 (
(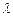
 为实数),证明:
为实数),证明: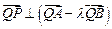 .
.(Ⅰ) 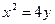 (Ⅱ) 见解析
(Ⅱ) 见解析
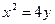 (Ⅱ) 见解析
(Ⅱ) 见解析(Ⅰ)解:由抛物线定义知
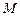 点的轨迹是以
点的轨迹是以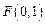 为焦点
为焦点 ,直线
,直线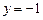 为准线的抛物线,………3分
为准线的抛物线,………3分
所以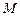 点的轨迹
点的轨迹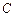 的方程是
的方程是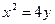 .……………………5分
.……………………5分
 (Ⅱ)证明:设直线AB的方程为
(Ⅱ)证明:设直线AB的方程为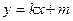 ,代入抛物线方程得:
,代入抛物线方程得: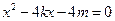 .
.
设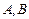 两点的坐标分别是
两点的坐标分别是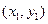 ,
,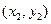 ,则
,则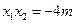 .………………7分
.………………7分
由点P满足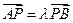 ,得
,得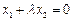 .
.
又点Q的坐标是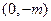 ,
, 从而
从而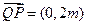 .
.
而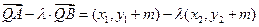 ,……………………9
,……………………9 分
分
 则
则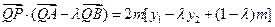
=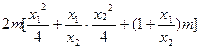
=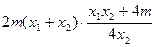 =
=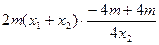 =0.
=0.
所以,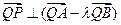 .……………………14分
.……………………14分

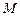 点的轨迹是以
点的轨迹是以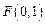 为焦点
为焦点 ,直线
,直线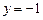 为准线的抛物线,………3分
为准线的抛物线,………3分所以
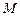 点的轨迹
点的轨迹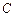 的方程是
的方程是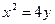 .……………………5分
.……………………5分 (Ⅱ)证明:设直线AB的方程为
(Ⅱ)证明:设直线AB的方程为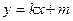 ,代入抛物线方程得:
,代入抛物线方程得: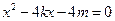 .
.设
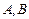 两点的坐标分别是
两点的坐标分别是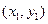 ,
,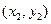 ,则
,则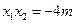 .………………7分
.………………7分由点P满足
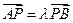 ,得
,得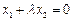 .
.又点Q的坐标是
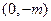 ,
, 从而
从而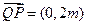 .
.而
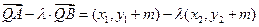 ,……………………9
,……………………9 分
分 则
则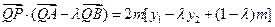
=
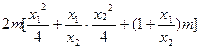
=
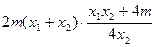 =
=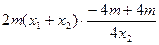 =0.
=0.所以,
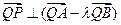 .……………………14分
.……………………14分


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
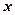 轴上,离心率为
轴上,离心率为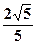 的椭圆的一个顶点是抛物线
的椭圆的一个顶点是抛物线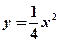 的焦点,过椭圆右焦点
的焦点,过椭圆右焦点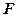 的直线
的直线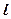 交椭圆于
交椭圆于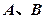 两点,交
两点,交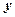 轴于点
轴于点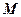 ,且
,且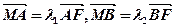 ,(1)求椭圆方程;(2)证明:
,(1)求椭圆方程;(2)证明: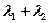 为定值
为定值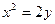 交于A、B两点,该抛物线在A、B两点处的两条切线交于点P。 (I)求点P的轨迹方程; (II)求△ABP的面积的最小值。
交于A、B两点,该抛物线在A、B两点处的两条切线交于点P。 (I)求点P的轨迹方程; (II)求△ABP的面积的最小值。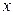 轴上,离心率
轴上,离心率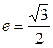 ,已知点
,已知点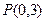 到这个椭圆上的点的最远距离是4,求这个椭圆的方程.
到这个椭圆上的点的最远距离是4,求这个椭圆的方程.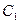 :
: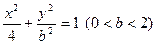 的离心率等于
的离心率等于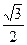 ,抛物线
,抛物线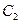 :
: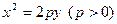 的焦点在椭圆的顶点上。(Ⅰ)求抛物线
的焦点在椭圆的顶点上。(Ⅰ)求抛物线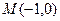 的直线
的直线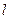 与抛物线
与抛物线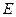 、
、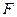 两点,又过
两点,又过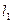 、
、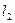 ,当
,当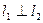 时,求直线
时,求直线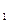 (-4,0)、F
(-4,0)、F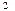 (4,0),并且椭圆和长轴长是双曲线实轴长的2倍,试求椭圆与双曲线交点的轨迹方程。
(4,0),并且椭圆和长轴长是双曲线实轴长的2倍,试求椭圆与双曲线交点的轨迹方程。 的一底边
的一底边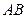 在平面
在平面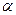 内,另一底边
内,另一底边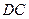 在平面
在平面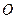 到平面
到平面 ,若
,若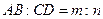 ,求
,求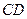 到平面
到平面