题目内容
(本小题满分12分)一束光线从点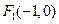 出发,经直线l:
出发,经直线l: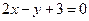 上一点
上一点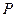 反射后,恰好穿过点
反射后,恰好穿过点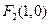 .(1)求
.(1)求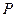 点的坐标;(2)求以
点的坐标;(2)求以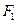 、
、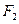 为焦点且过点
为焦点且过点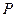 的椭圆
的椭圆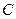 的方程; (3)设点
的方程; (3)设点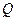 是椭圆
是椭圆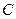 上除长轴两端点外的任意一点,试问在
上除长轴两端点外的任意一点,试问在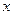 轴上是否存在两定点
轴上是否存在两定点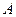 、
、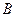 ,使得直线
,使得直线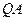 、
、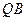 的斜率之积为定值?若存在,请求出定值,并求出所有满足条件的定点
的斜率之积为定值?若存在,请求出定值,并求出所有满足条件的定点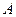 、
、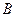 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
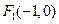 出发,经直线l:
出发,经直线l: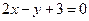 上一点
上一点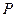 反射后,恰好穿过点
反射后,恰好穿过点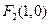 .(1)求
.(1)求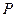 点的坐标;(2)求以
点的坐标;(2)求以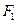 、
、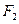 为焦点且过点
为焦点且过点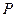 的椭圆
的椭圆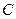 的方程; (3)设点
的方程; (3)设点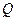 是椭圆
是椭圆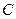 上除长轴两端点外的任意一点,试问在
上除长轴两端点外的任意一点,试问在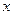 轴上是否存在两定点
轴上是否存在两定点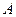 、
、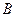 ,使得直线
,使得直线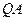 、
、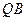 的斜率之积为定值?若存在,请求出定值,并求出所有满足条件的定点
的斜率之积为定值?若存在,请求出定值,并求出所有满足条件的定点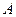 、
、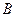 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.(Ⅰ)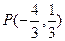 (Ⅱ)
(Ⅱ) 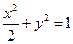 (Ⅲ)
(Ⅲ)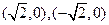
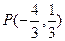 (Ⅱ)
(Ⅱ) 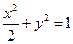 (Ⅲ)
(Ⅲ)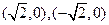
(1)设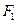 关于l的对称点为
关于l的对称点为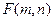 ,则
,则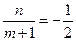 且
且 ,
,
解得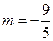 ,
,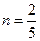 ,即
,即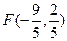 ,故直线
,故直线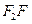 的方程为
的方程为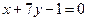 .
.
由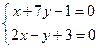 ,解得
,解得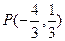 . ------------------------3分
. ------------------------3分
(2)因为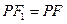 ,根据椭圆定义,得
,根据椭圆定义,得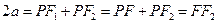
 ,所以
,所以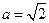 .又
.又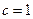 ,所以
,所以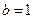 .
.
所以椭圆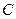 的方程为
的方程为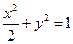 . --------------------7分
. --------------------7分
(3)假设存在两定点为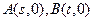 ,使得对于椭圆上任意一点
,使得对于椭圆上任意一点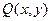 (除长轴两端点)都有
(除长轴两端点)都有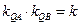 (
(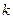 为定值),即
为定值),即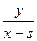 ·
·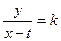 ,将
,将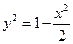 代入并整理得
代入并整理得 …(*).由题意,(*)式对任意
…(*).由题意,(*)式对任意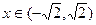 恒成立,所以
恒成立,所以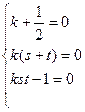 ,解之得
,解之得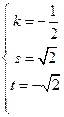 或
或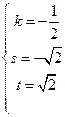 .
.
所以有且只有两定点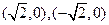 ,使得
,使得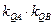 为定值
为定值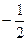 . ----------12分
. ----------12分
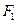 关于l的对称点为
关于l的对称点为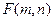 ,则
,则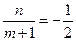 且
且 ,
,解得
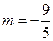 ,
,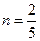 ,即
,即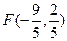 ,故直线
,故直线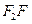 的方程为
的方程为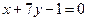 .
.由
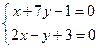 ,解得
,解得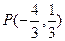 . ------------------------3分
. ------------------------3分(2)因为
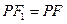 ,根据椭圆定义,得
,根据椭圆定义,得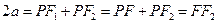
 ,所以
,所以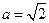 .又
.又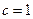 ,所以
,所以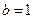 .
.所以椭圆
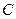 的方程为
的方程为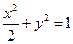 . --------------------7分
. --------------------7分(3)假设存在两定点为
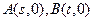 ,使得对于椭圆上任意一点
,使得对于椭圆上任意一点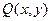 (除长轴两端点)都有
(除长轴两端点)都有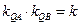 (
(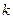 为定值),即
为定值),即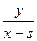 ·
·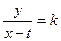 ,将
,将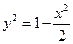 代入并整理得
代入并整理得 …(*).由题意,(*)式对任意
…(*).由题意,(*)式对任意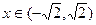 恒成立,所以
恒成立,所以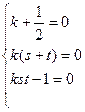 ,解之得
,解之得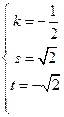 或
或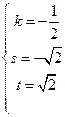 .
.所以有且只有两定点
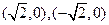 ,使得
,使得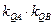 为定值
为定值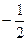 . ----------12分
. ----------12分
练习册系列答案
相关题目
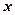 轴上,离心率为
轴上,离心率为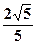 的椭圆的一个顶点是抛物线
的椭圆的一个顶点是抛物线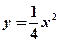 的焦点,过椭圆右焦点
的焦点,过椭圆右焦点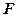 的直线
的直线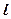 交椭圆于
交椭圆于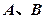 两点,交
两点,交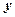 轴于点
轴于点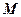 ,且
,且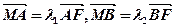 ,(1)求椭圆方程;(2)证明:
,(1)求椭圆方程;(2)证明: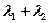 为定值
为定值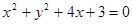 与抛物线
与抛物线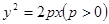 的准线相切,则
的准线相切,则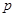 = .
= .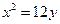 的切线垂直于直线
的切线垂直于直线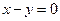 ,则切线方程为 .
,则切线方程为 .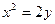 交于A、B两点,该抛物线在A、B两点处的两条切线交于点P。 (I)求点P的轨迹方程; (II)求△ABP的面积的最小值。
交于A、B两点,该抛物线在A、B两点处的两条切线交于点P。 (I)求点P的轨迹方程; (II)求△ABP的面积的最小值。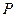 到定点
到定点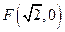 的距离与点
的距离与点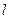 :
: 的距离之比为
的距离之比为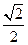 .
.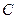 的方程;
的方程;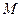 、
、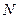 是直线
是直线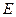 与点
与点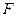 关于原点
关于原点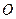 对称,若
对称,若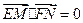 ,求
,求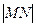 的最小值.
的最小值.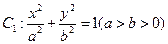 的左、右焦点分别为
的左、右焦点分别为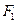 、
、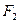 ,其中
,其中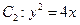 的焦点,
的焦点,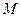 是
是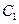 与
与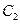 在第一象限的交点,且
在第一象限的交点,且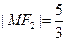 .(Ⅰ)求椭圆
.(Ⅰ)求椭圆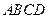 的顶点A﹑C在椭圆
的顶点A﹑C在椭圆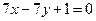 上,求直线
上,求直线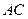 的方程.
的方程.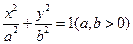 的焦点坐
的焦点坐 标为
标为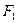 (
(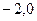 ),点M(
),点M(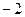 ,
,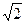 )在椭圆E上
)在椭圆E上 (1)求椭圆E的方程;(2)O为坐标原点,⊙
(1)求椭圆E的方程;(2)O为坐标原点,⊙ 的任意一条切线与椭圆E有两个交点
的任意一条切线与椭圆E有两个交点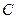 ,
,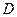 且
且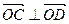 ,求⊙
,求⊙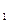 (-4,0)、F
(-4,0)、F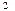 (4,0),并且椭圆和长轴长是双曲线实轴长的2倍,试求椭圆与双曲线交点的轨迹方程。
(4,0),并且椭圆和长轴长是双曲线实轴长的2倍,试求椭圆与双曲线交点的轨迹方程。