题目内容
设函数f(x)=|x-4|+|x-a|(a<4).
(Ⅰ)若f(x)的最小值为3,求a值;
(Ⅱ)求不等式f(x)≥3-x的解集.
(Ⅰ)若f(x)的最小值为3,求a值;
(Ⅱ)求不等式f(x)≥3-x的解集.
(1)因为函数f(x)=|x-4|+|x-a|≥|(x-4)-(x-a)|=|a-4|,
因为a<4,所以当且仅当 a≤x≤4时等号成立,故|a-4|=3,即a=1.
(2)不等式f(x)≥3-x,即不等式|x-4|+|x-a|≥3-x,a<4,
①当x<a时,原不等式可化为 4-x+a-x≥3-x,x≤a+1.
所以,当x<a时,原不等式成立.
②当a≤x≤4时,原不等式可化为4-x+x-a≥3-x,
即x≥a-1,所以,当a≤x≤4时,原不等式成立.
③当x>4时,原不等式可化为 x-4+x-a≥3-x,
即x≥
由于a<4时 4>
.
所以,当x>4时,原不等式成立.
综合①②③可知:不等式f(x)≥3-x的解集为R.
因为a<4,所以当且仅当 a≤x≤4时等号成立,故|a-4|=3,即a=1.
(2)不等式f(x)≥3-x,即不等式|x-4|+|x-a|≥3-x,a<4,
①当x<a时,原不等式可化为 4-x+a-x≥3-x,x≤a+1.
所以,当x<a时,原不等式成立.
②当a≤x≤4时,原不等式可化为4-x+x-a≥3-x,
即x≥a-1,所以,当a≤x≤4时,原不等式成立.
③当x>4时,原不等式可化为 x-4+x-a≥3-x,
即x≥
| a+7 |
| 3 |
| a+7 |
| 3 |
所以,当x>4时,原不等式成立.
综合①②③可知:不等式f(x)≥3-x的解集为R.

练习册系列答案
相关题目
 的解集为 .
的解集为 .
 对一切
对一切 都成立,则
都成立,则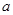 的取值范围是( )
的取值范围是( )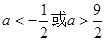

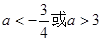

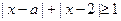 对任意实数
对任意实数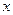 均成立,求实数
均成立,求实数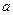 的取值范围
的取值范围 的不等式
的不等式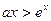 在
在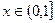 上恒成立,则
上恒成立,则 的取值范围是 。
的取值范围是 。