题目内容
已知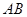 为半圆
为半圆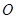 的直径,
的直径,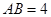 ,
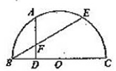
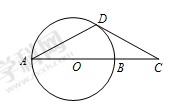
,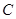 为半圆上一点,过点
为半圆上一点,过点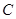 作半圆的切线
作半圆的切线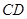 ,过
,过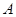 点作
点作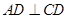 于
于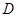 ,交半圆于点
,交半圆于点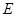 ,
,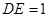 .
.
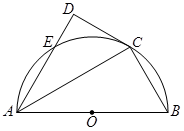
(1)求证: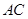 平分
平分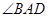 ;
;
(2)求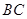 的长.
的长.
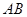 为半圆
为半圆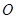 的直径,
的直径,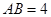 ,
,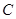 为半圆上一点,过点
为半圆上一点,过点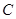 作半圆的切线
作半圆的切线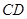 ,过
,过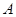 点作
点作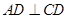 于
于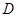 ,交半圆于点
,交半圆于点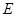 ,
,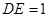 .
.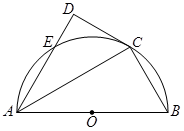
(1)求证:
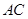 平分
平分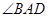 ;
;(2)求
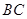 的长.
的长.(1)参考解析;(2)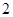
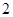
试题分析:(1)需证明
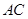 平分
平分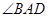 ,通过连接OC,EC.由题意可得直线AD∥OC.从而可得角DAC等于角ACO.又由于三角形AOC是等腰三角形.即可得到结论.
,通过连接OC,EC.由题意可得直线AD∥OC.从而可得角DAC等于角ACO.又由于三角形AOC是等腰三角形.即可得到结论.(2)由(1)的结论∠DAC=∠CAB.以及再根据弦切角与所夹的弧对的圆周角相等即可得到三角形DEC相似三角形CBA.
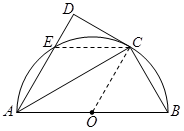
(1)连接
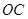 ,因为
,因为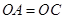 ,
,所以
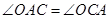 .
.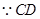 为半圆的切线,∴
为半圆的切线,∴ .
.∵
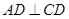 ,
,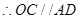 .
.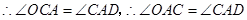 .
.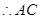 平分
平分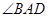 . 5分
. 5分(2)连接
 ,由(1)得
,由(1)得 ,∴
,∴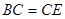 .
.∵
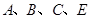 四点共圆.∴
四点共圆.∴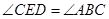 .
.∵AB是圆O的直径,∴
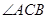 是直角.∴
是直角.∴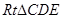 ∽
∽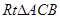 ,
,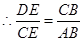 .∴
.∴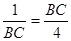
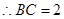 . 10分
. 10分
练习册系列答案
相关题目
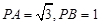 ,则
,则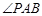 =_________.
=_________.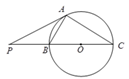
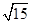
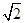
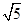
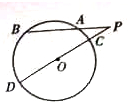
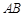 是圆
是圆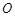 的直径,延长
的直径,延长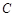 ,使
,使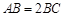 ,且
,且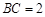 ,
,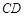 是圆
是圆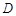 ,连接
,连接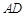 ,则
,则 ________,
________,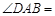 ________.
________.
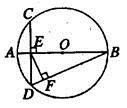
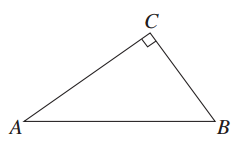
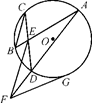
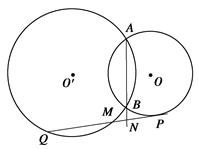
 是半圆周上的两个三等分点,直径
是半圆周上的两个三等分点,直径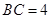 ,
,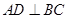 ,垂足为D,
,垂足为D, 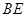 与
与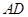 相交与点F,则
相交与点F,则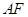 的长为 。
的长为 。