题目内容
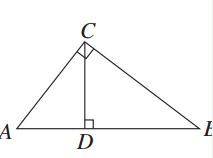
有一块直角三角形木板,如图所示,∠C=90°,AB=5 cm,BC=3 cm,AC=4 cm,根据需要,要把它加工成一个面积最大的正方形木板,设计一个方案,应怎样裁才能使正方形木板面积最大,并求出这个正方形木板的边长.

边长为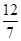 cm,见解析
cm,见解析
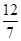 cm,见解析
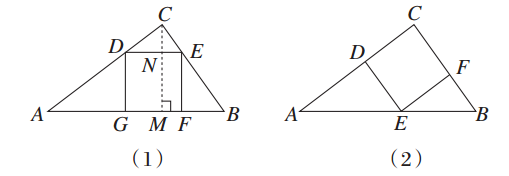
cm,见解析解:如图(1)所示,设正方形DEFG的边长为x cm,过点C作CM⊥AB于M,交DE于N,
因为S△ABC=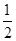 AC·BC=
AC·BC=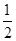 AB·CM,
AB·CM,
所以AC·BC=AB·CM,即3×4=5·CM.所以CM=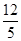 .
.
因为DE∥AB,所以△CDE∽△CAB.
所以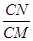 =
=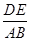 ,即
,即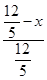 =
= .
.
所以x=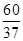 .
.
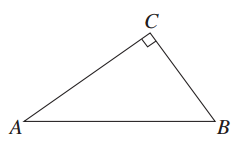
如图(2)所示,设正方形CDEF的边长为y cm,因为EF∥AC,所以△BEF∽△BAC.
所以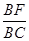 =
=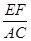 ,即
,即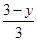 =
=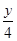 .所以y=
.所以y=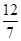 .
.
因为x=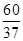 ,y=
,y=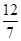 =
=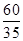 ,所以x<y.
,所以x<y.
所以当按图(2)的方法裁剪时,正方形面积最大,其边长为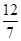 cm.
cm.
因为S△ABC=
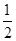 AC·BC=
AC·BC=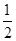 AB·CM,
AB·CM,所以AC·BC=AB·CM,即3×4=5·CM.所以CM=
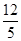 .
.因为DE∥AB,所以△CDE∽△CAB.
所以
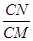 =
=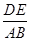 ,即
,即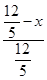 =
= .
.所以x=
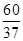 .
.
如图(2)所示,设正方形CDEF的边长为y cm,因为EF∥AC,所以△BEF∽△BAC.
所以
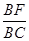 =
=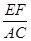 ,即
,即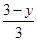 =
=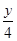 .所以y=
.所以y=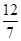 .
.因为x=
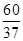 ,y=
,y=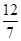 =
=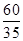 ,所以x<y.
,所以x<y.所以当按图(2)的方法裁剪时,正方形面积最大,其边长为
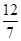 cm.
cm.
练习册系列答案
 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
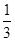 AC,BD=
AC,BD=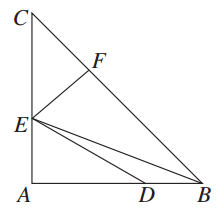
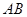 为半圆
为半圆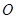 的直径,
的直径,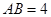 ,
, 为半圆上一点,过点
为半圆上一点,过点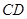 ,过
,过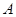 点作
点作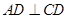 于
于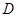 ,交半圆于点
,交半圆于点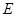 ,
,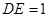 .
.
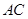 平分
平分 ;
; 的长.
的长.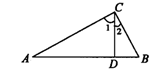
 作圆的切线
作圆的切线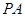 (
(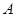 为切点),再作割线
为切点),再作割线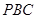 分别交圆于
分别交圆于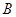 、
、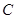 , 若
, 若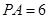 ,
,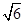 ∶3
∶3