题目内容
过抛物线y2=2px(p>0)焦点的直线交抛物线于A、B两点,则|AB|的最小值为( )
A.
| B.p | C.2p | D.无法确定 |
抛物线y2=2px(p>0)焦点坐标为(
,0),则
斜率存在时,设方程为y=k(x-
),代入抛物线y2=2px可得k2x2-(k2p+2p)x+
=0,
设A(x1,y1),B(x2,y2),则x1+x2=p+
,
∴|AB|=x1+x2+p=2p+
>2p,
斜率不存在时,方程为x=
,|AB|=x1+x2+p=2p,
∴|AB|的最小值为2p.
故选:C.
| p |
| 2 |
斜率存在时,设方程为y=k(x-
| p |
| 2 |
| k2p2 |
| 4 |
设A(x1,y1),B(x2,y2),则x1+x2=p+
| 2p |
| k2 |
∴|AB|=x1+x2+p=2p+
| 2p |
| k2 |
斜率不存在时,方程为x=
| p |
| 2 |
∴|AB|的最小值为2p.
故选:C.

练习册系列答案
相关题目
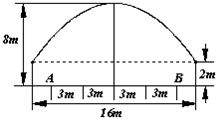
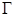 上的点到点
上的点到点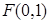 的距离比它到直线
的距离比它到直线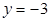 的距离小2.
的距离小2.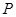 处的切线
处的切线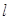 与
与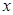 轴交于点
轴交于点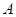 .直线
.直线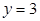 分别与直线
分别与直线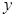 轴交于点
轴交于点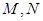 ,以
,以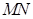 为直径作圆
为直径作圆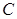 ,过点
,过点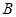 ,试探究:当点
,试探究:当点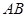 的长度是否发生变化?证明你的结论.
的长度是否发生变化?证明你的结论.