Question

【题目】设直线l的方程为(a＋1)x＋y－2－a＝0(a∈R)．

(1)若直线l在两坐标轴上的截距相等，则直线l的方程为__________________________；

(2)若a>－1，直线l与x、y轴分别交于M、N两点，O为坐标原点，则△OMN的面积取最小值时，直线l对应的方程为________________.

Answer 1

【答案】 x－y＝0或x＋y－2＝0 x＋y－2＝0

【解析】(1)①当直线l经过坐标原点时，

可得a＋2＝0，

解得a＝－2。

所以直线l的方程为－x＋y＝0，即x－y＝0；

②当直线l不经过坐标原点，即a≠－2且a≠－1时，

由条件得，

解得a＝0，

所以直线l的方程为x＋y－2＝0．

综上可得直线l的方程为x－y＝0或x＋y－2＝0．

(2)在(a＋1)x＋y－2－a＝0（a>－1）中，

令，得；令，得．

所以．

由于，得．

所以

．

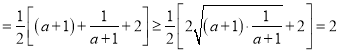当且仅当，即a＝0时等号成立．

此时直线l的方程为x＋y－2＝0．

答案：(1) x－y＝0或x＋y－2＝0 (2) x＋y－2＝0