题目内容
【题目】已知函数
在
与
时都取得极值.（1）求
的值；（2）若对
， 
恒成立，求
的取值范围
【答案】(1) 
(2) 
【解析】试题分析：（1）求出导函数，通过
和
为
的两根，得到方程组求解即可；（2）化简函数
，求出导函数，通过当
时，当
时，当
时， 
，当
时， 
，判断函数的单调性，求出函数的极值，然后求解
的取值范围.
试题解析：（1）∵
，由已知条件可知： 
和1为
的两根，
由韦达定理得：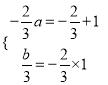 
，∴
， 
（2）由（1）得： 
，由题知：当
(－2， 
)时， 
∴函数
在区间(－2， 
)上是增函数；
当
(
，1)时， 
在(
，1)上是减函数；
当
(1，2)时， 
，∴函数
在(1，2)上是增函数，
∴当
时， 
；当
时， 
∵
，∴
[－2，2]时， 
，
由
在
[－2，2]时， 
恒成立得： 
由此解得： 
∴
的取值范围为：(
， 
]∪[2， 
)
练习册系列答案
备战中考寒假系列答案
相关题目
