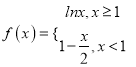Question

【题目】已知函数f(x)＝x2－ax－alnx(a∈R)．

(1)若函数f(x)在x＝1处取得极值，求a的值；

(2)在(1)的条件下，求证：f(x)≥－＋－4x＋.

Answer 1

【答案】(1) a＝1.(2) 见解析.

【解析】试题分析：（1）根据极值的定义即导函数的变号零点，求导使得f′(1)＝0，解得a＝1；并检验a＝1时1是函数的变号零点即可（2）构造函数g(x)＝f(x)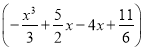－，研究这个函数的单调性，使得这个函数的最小值大于等于0即可.

解析：

(1)解　f′(x)＝2x－a－，由题意可得f′(1)＝0，解得a＝1.经检验，a＝1时f(x)在x＝1处取得极值，所以a＝1.

(2)证明　由(1)知，f(x)＝x2－x－lnx，

令g(x)＝f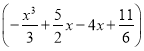(x)－

＝－＋3x－lnx－，

由g′(x)＝x2－3x＋3－＝－3(x－1)＝ (x>0)，可知g(x)在(0,1)上是减函数，

在(1，＋∞)上是增函数，所以g(x)≥g(1)＝0，所以f(x)≥－＋－4x＋成立．