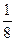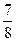题目内容
设函数f(x)=ax+
(x>1),若a是从1,2,3三数中任取一个,b是从2,3,4,5四数中任取一个,那么f(x)>b恒成立的概率为( )
| x |
| x-1 |
A.
| B.
| C.
| D.
|
x>1,a>0,f(x)=ax+
=ax+
+1
=a(x-1)+
+1+a≥2
+1+a=(
+1)2,
当且仅当x=
+1>1时,取“=”,
∴f(x)min=(
+1)2,
于是f(x)>b恒成立就转化为(
+1)2>b成立.
设事件A:“f(x)>b恒成立”,则
基本事件总数为12个,即
(1,2),(1,3),(1,4),(1,5);
(2,2),(2,3),(2,4),(2,5);
(3,2),(3,3),(3,4),(3,5);
事件A包含事件:(1,2),(1,3);
(2,2),(2,3),(2,4),(2,5);
(3,2),(3,3),(3,4),(3,5)共10个
由古典概型得P(A)=
=
,
故选D.
| x-1+1 |
| x-1 |
| 1 |
| x-1 |
=a(x-1)+
| 1 |
| x-1 |
| a |
| a |
当且仅当x=
|
∴f(x)min=(
| a |
于是f(x)>b恒成立就转化为(
| a |
设事件A:“f(x)>b恒成立”,则
基本事件总数为12个,即
(1,2),(1,3),(1,4),(1,5);
(2,2),(2,3),(2,4),(2,5);
(3,2),(3,3),(3,4),(3,5);
事件A包含事件:(1,2),(1,3);
(2,2),(2,3),(2,4),(2,5);
(3,2),(3,3),(3,4),(3,5)共10个
由古典概型得P(A)=
| 10 |
| 12 |
| 5 |
| 6 |
故选D.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目