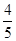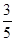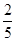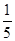题目内容
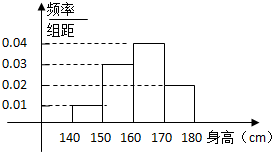
某中学对高三年级进行身高统计,测量随机抽取的20名学生的身高,其频率分布直方图如下(单位:cm)
(1)根据频率分布直方图,求出这20名学生身高中位数的估计值和平均数的估计值.
(2)在身高为140-160的学生中任选2个,求至少有一人的身高在150-160之间的概率.
(1)根据频率分布直方图,求出这20名学生身高中位数的估计值和平均数的估计值.
(2)在身高为140-160的学生中任选2个,求至少有一人的身高在150-160之间的概率.

(1)中位数的左边和右边的直方图的面积相等,由此可以估计中位数的值,∵0.1+0.3+0.04×2.5=0.5
所以中位数的估计值为162.5.
平均数的估计值等于频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和.
则平均数的估计值为145×0.1+155×0.3+165×0.4+175×0.2=162,
(2)这20名学生中,身高在140-150之间的有2个,分别为A,B,身高在150-160之间的有6人,
从这8人中任选2个,有
=28种选法,
两个身高都在140---150之间的选法有1种选法,
所以至少有一个人在150-160之间的选法有28-1=27,
故至少有一人的身高在150-160之间的概率为
.
所以中位数的估计值为162.5.
平均数的估计值等于频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和.
则平均数的估计值为145×0.1+155×0.3+165×0.4+175×0.2=162,
(2)这20名学生中,身高在140-150之间的有2个,分别为A,B,身高在150-160之间的有6人,
从这8人中任选2个,有
| C | 28 |
两个身高都在140---150之间的选法有1种选法,
所以至少有一个人在150-160之间的选法有28-1=27,
故至少有一人的身高在150-160之间的概率为
| 27 |
| 28 |

练习册系列答案
相关题目

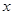 ,
, 的值介于1到2之间的概率为( )
的值介于1到2之间的概率为( )


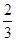
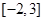 上随机选取一个数
上随机选取一个数 ,则
,则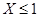 的概率为( )
的概率为( )