题目内容
已知关于x的一元二次方程x2-2ax+b2=0.
(1)若a是从0、1、2、3四个数中任取的一个数,b是从0、1、2三个数中任取的一个数,求上述方程没有实根的概率;
(2)若a是从区间[0,3]内任取的一个数,b是从区间[0,2]内任取的一个数,求上述方程没有实根的概率.
(1)若a是从0、1、2、3四个数中任取的一个数,b是从0、1、2三个数中任取的一个数,求上述方程没有实根的概率;
(2)若a是从区间[0,3]内任取的一个数,b是从区间[0,2]内任取的一个数,求上述方程没有实根的概率.
(1)设事件A为“方程x2-2ax+b2=0无实根”;--------(1分)
当△=4a2-4b2=4(a2-b2)<0,即a<b时,方程x2-2ax+b2=0无实根.---------(3分)
所有的(a,b)共12个:(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),
(2,0),(2,1),(2,2),(3,0),(3,1),(3,2).
其中,第一个数表示a的取值,第二个数表示b的取值.
事件A包含3个基本事件(0,1),(0,2),(1,2),
由于每个基本事件发生的可能性都相同,------(4分)
∴事件A发生的概率P(A)=
=
.---------(6分)
答:方程x2-2ax+b2=0没有实根的概率为
.-------(7分)
(2)设事件B为“方程x2-2ax+b2=0无实根”;----(8分)
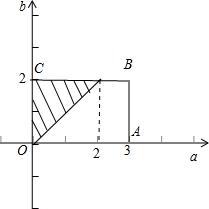
如图,试验的所有基本事件所构成的区域为矩形OABC:{(a,b)|0≤a≤3,0≤b≤2},
其中构成事件B的区域为三角形OEC,即{(a,b)|0≤a≤3,0≤b≤2,a<b},
由于点(a,b)落在区域内的每一点是随机的,----------(10分)
∴事件B发生的概率P(B)=
=
=
.-------(13分)
答:方程x2-2ax+b2=0没有实根的概率为
.--------(14分)
当△=4a2-4b2=4(a2-b2)<0,即a<b时,方程x2-2ax+b2=0无实根.---------(3分)
所有的(a,b)共12个:(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),
(2,0),(2,1),(2,2),(3,0),(3,1),(3,2).
其中,第一个数表示a的取值,第二个数表示b的取值.
事件A包含3个基本事件(0,1),(0,2),(1,2),
由于每个基本事件发生的可能性都相同,------(4分)
∴事件A发生的概率P(A)=
| 3 |
| 12 |
| 1 |
| 4 |
答:方程x2-2ax+b2=0没有实根的概率为
| 1 |
| 4 |
(2)设事件B为“方程x2-2ax+b2=0无实根”;----(8分)
如图,试验的所有基本事件所构成的区域为矩形OABC:{(a,b)|0≤a≤3,0≤b≤2},
其中构成事件B的区域为三角形OEC,即{(a,b)|0≤a≤3,0≤b≤2,a<b},
由于点(a,b)落在区域内的每一点是随机的,----------(10分)
∴事件B发生的概率P(B)=
| S△OEC |
| SOABC |
| ||
| 3×2 |
| 1 |
| 3 |
答:方程x2-2ax+b2=0没有实根的概率为
| 1 |
| 3 |


练习册系列答案
相关题目
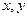 用
用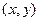 的形式列出所有的基本事件, 其中
的形式列出所有的基本事件, 其中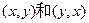 视为同一事件,并求
视为同一事件,并求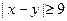 的事件A的概率。
的事件A的概率。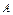 与
与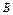 的差集
的差集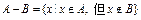 。记“从集合
。记“从集合 ”为事件
”为事件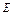 ,“从集合
,“从集合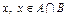 ”为事件
”为事件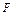 ;
;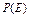 为事件
为事件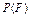 为事件
为事件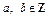 ,且
,且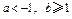 时,设集合
时,设集合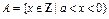 ,集合
,集合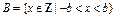 。给出下列判断: ①当
。给出下列判断: ①当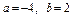 时,
时,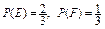 ;②总有
;②总有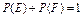 ;③若
;③若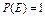 ,则
,则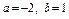 ;④
;④