题目内容
在△ABC中,已知a:b:c=3:4:5,在边AB上任取一点M,则△AMC是钝角三角形的概率为______.
如图所示:过点C作CH⊥AB,H为垂足,
显然,当点M位于线段AH上时,∠AMC为钝角,
△AMC是钝角三角形,
根据
•AC•BC=
AB•CH,可得
×3×4=
×5×CH,
解得CH=
.
再由勾股定理求得AH=
=
=
,
故△AMC是钝角三角形的概率为
=
=
,
故答案为
.

显然,当点M位于线段AH上时,∠AMC为钝角,
△AMC是钝角三角形,
根据
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得CH=
| 12 |
| 5 |
再由勾股定理求得AH=
| AC2-CH2 |
16-
|
| 16 |
| 5 |
故△AMC是钝角三角形的概率为
| AH |
| AB |
| ||
| 5 |
| 16 |
| 25 |
故答案为
| 16 |
| 25 |


练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
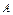 与
与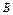 的差集
的差集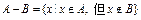 。记“从集合
。记“从集合 ”为事件
”为事件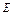 ,“从集合
,“从集合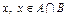 ”为事件
”为事件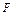 ;
;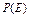 为事件
为事件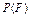 为事件
为事件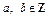 ,且
,且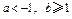 时,设集合
时,设集合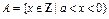 ,集合
,集合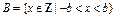 。给出下列判断: ①当
。给出下列判断: ①当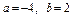 时,
时,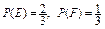 ;②总有
;②总有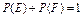 ;③若
;③若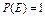 ,则
,则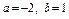 ;④
;④