题目内容
四面体 中,
中,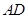 与
与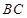 互相垂直,
互相垂直,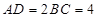 ,且
,且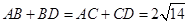 ,则四面体
,则四面体 的体积的最大值是( ) .
的体积的最大值是( ) .
 中,
中,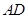 与
与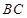 互相垂直,
互相垂直,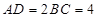 ,且
,且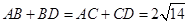 ,则四面体
,则四面体 的体积的最大值是( ) .
的体积的最大值是( ) .| A.4 | B.2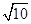 | C.5 | D.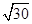 |
A
试题分析:

作
 于
于 ,连接
,连接 ,又因为
,又因为 ,则
,则 平面
平面 ,所以
,所以 ,
,由题设
 ,
, 与
与 都是在以
都是在以 为焦点的椭圆上,且
为焦点的椭圆上,且 都垂直于焦距
都垂直于焦距 ,显然
,显然 ,所以
,所以 .
.取
 中点
中点 ,
, ,
, ,要求四面体
,要求四面体 的体积的最大值,因为
的体积的最大值,因为 是定值,只需
是定值,只需 的面积最大,因为
的面积最大,因为 是定值,所以只需高
是定值,所以只需高 最大即可,
最大即可, ,
, 为定值,所以
为定值,所以 最大即
最大即 最大,点
最大,点 在以
在以 为焦点的椭圆上,所以当
为焦点的椭圆上,所以当 为中点,即
为中点,即 短轴长时,
短轴长时, 最大,
最大, ,所以短轴长为
,所以短轴长为 ,即
,即 ,此时
,此时 =
= ,
, ,故选A.
,故选A.
练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
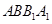 是圆柱体的轴截面,
是圆柱体的轴截面, 分别是下底面圆和上底面圆的圆心,母线长与底面圆的直径长之比为
分别是下底面圆和上底面圆的圆心,母线长与底面圆的直径长之比为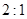 ,且该圆柱体的体积为
,且该圆柱体的体积为 ,如图所示.
,如图所示.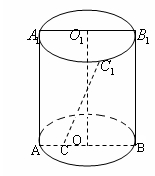
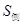 的值;
的值;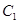 是半圆弧
是半圆弧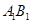 的中点,点
的中点,点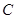 在半径
在半径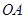 上,且
上,且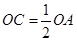 ,异面直线
,异面直线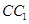 与
与 所成的角为
所成的角为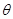 ,求
,求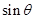 的值.
的值.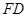 垂直于矩形
垂直于矩形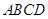 所在平面,
所在平面,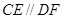 ,
,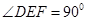 .
.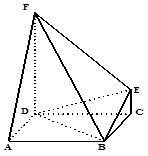
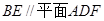 ;
;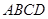 的一个边
的一个边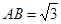 ,
,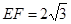 ,则另一边
,则另一边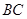 的长为何值时,三棱锥
的长为何值时,三棱锥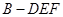 的体积为
的体积为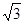 ?
?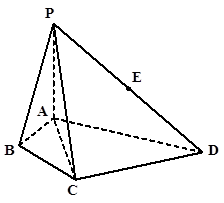
 A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.
A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.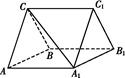
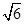 ,求三棱柱ABC
,求三棱柱ABC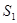 、
、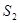 ,则
,则 中,
中, ,
, ,
, ,二面角
,二面角 的余弦值是
的余弦值是 ,若
,若 都在同一球面上,则该球的表面积是.
都在同一球面上,则该球的表面积是.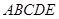 的体积为( )
的体积为( )
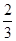
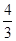
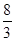
 的顶点都在半径为4的球
的顶点都在半径为4的球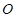 的球面上,且
的球面上,且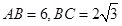 ,则棱锥
,则棱锥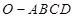 的体积为 。
的体积为 。