题目内容
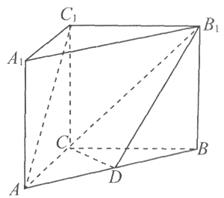
如图,三棱柱ABC A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.
A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.
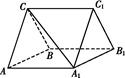
(1)证明:AB⊥A1C;
(2)若AB=CB=2,A1C=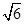 ,求三棱柱ABC
,求三棱柱ABC A1B1C1的体积.
A1B1C1的体积.
 A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.
A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.
(1)证明:AB⊥A1C;
(2)若AB=CB=2,A1C=
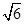 ,求三棱柱ABC
,求三棱柱ABC A1B1C1的体积.
A1B1C1的体积.(1)见解析 (2)3
(1)证明:取AB的中点O,连接OC,OA1,A1B.
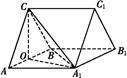
因为CA=CB,所以OC⊥AB.
由于AB=AA1,∠BAA1=60°,
故△AA1B为等边三角形,
所以OA1⊥AB.
因为OC∩OA1=O,
所以AB⊥平面OA1C.
又A1C?平面OA1C,故AB⊥A1C.
(2)解:由题设知△ABC与△AA1B都是边长为2的等边三角形,所以OC=OA1=
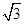 .
.又A1C=
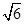 ,则A1C2=OC2+O
,则A1C2=OC2+O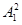 ,故OA1⊥OC.
,故OA1⊥OC.因为OC∩AB=O,所以OA1⊥平面ABC,OA1为三棱柱ABC
 A1B1C1的高.
A1B1C1的高.又△ABC的面积S△ABC=
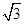 ,故三棱柱ABC
,故三棱柱ABC A1B1C1的体积V=S△ABC×OA1=3.
A1B1C1的体积V=S△ABC×OA1=3.
练习册系列答案
相关题目
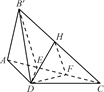
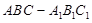 中,
中,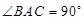 ,
,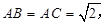
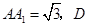 是
是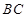 中点,
中点,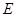 是
是 中点.
中点.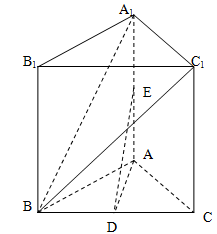
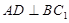 ;
;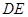 ∥面
∥面 .
.
 中,
中,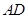 与
与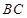 互相垂直,
互相垂直,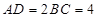 ,且
,且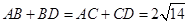 ,则四面体
,则四面体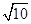
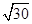
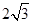 ,底面是等边三角形,则这个三棱锥的体积为( )
,底面是等边三角形,则这个三棱锥的体积为( )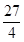
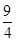
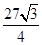
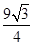
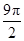 ,则正方体的棱长为 .
,则正方体的棱长为 . A1B1C1D1中,AB=AD=3cm,AA1=2cm,则四棱锥A
A1B1C1D1中,AB=AD=3cm,AA1=2cm,则四棱锥A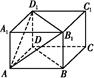
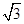 的正三角形,侧棱垂直于底面,且该三棱柱的外接球的体积为
的正三角形,侧棱垂直于底面,且该三棱柱的外接球的体积为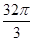 ,则该三棱柱的体积为________.
,则该三棱柱的体积为________.