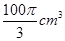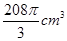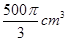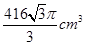题目内容
已知矩形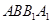 是圆柱体的轴截面,
是圆柱体的轴截面,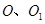 分别是下底面圆和上底面圆的圆心,母线长与底面圆的直径长之比为
分别是下底面圆和上底面圆的圆心,母线长与底面圆的直径长之比为 ,且该圆柱体的体积为
,且该圆柱体的体积为 ,如图所示.
,如图所示.
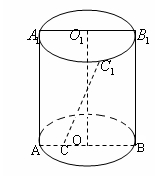
(1)求圆柱体的侧面积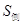 的值;
的值;
(2)若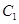 是半圆弧
是半圆弧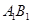 的中点,点
的中点,点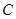 在半径
在半径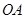 上,且
上,且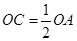 ,异面直线
,异面直线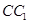 与
与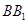 所成的角为
所成的角为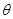 ,求
,求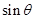 的值.
的值.
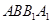 是圆柱体的轴截面,
是圆柱体的轴截面,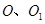 分别是下底面圆和上底面圆的圆心,母线长与底面圆的直径长之比为
分别是下底面圆和上底面圆的圆心,母线长与底面圆的直径长之比为 ,且该圆柱体的体积为
,且该圆柱体的体积为 ,如图所示.
,如图所示.
(1)求圆柱体的侧面积
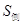 的值;
的值;(2)若
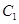 是半圆弧
是半圆弧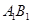 的中点,点
的中点,点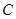 在半径
在半径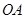 上,且
上,且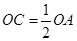 ,异面直线
,异面直线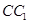 与
与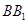 所成的角为
所成的角为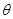 ,求
,求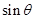 的值.
的值.(1) ;(2)
;(2)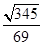 .
.
 ;(2)
;(2)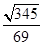 .
.试题分析:要求圆柱侧面积,必须求得圆柱的底面半径
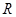 和母线长
和母线长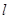 ,这里可由已知体积求得,首先由题意
,这里可由已知体积求得,首先由题意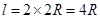 ,
,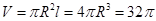 ,
,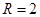 ,由此可得侧面积;(2)要求异面直线所成的角,关键是作出这个角,由于待求夹角的两异面直线中有一条是圆柱的高,因此平行线很好作,例如圆柱的母线一定与高平行,可取过
,由此可得侧面积;(2)要求异面直线所成的角,关键是作出这个角,由于待求夹角的两异面直线中有一条是圆柱的高,因此平行线很好作,例如圆柱的母线一定与高平行,可取过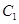 的母线,得夹角,也可取上底面半径
的母线,得夹角,也可取上底面半径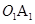 的中点
的中点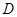 ,则
,则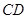 ∥
∥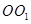 ,
,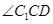 就是我们所要求的角,然后在
就是我们所要求的角,然后在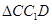 中解得.
中解得.试题解析:(1)设圆柱的底面圆的半径为
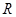 ,依据题意,有
,依据题意,有 ,
,∴
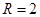 .
.∴
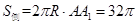 .
.(2)设
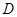 是线段
是线段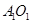 的中点,联结
的中点,联结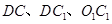 ,则
,则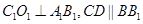 .
.因此,
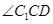 就是异面直线
就是异面直线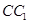 与
与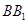 所成的角,即
所成的角,即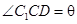 .
.又
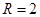 ,
,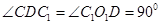 ,
,∴
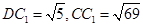 .
.∴
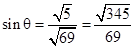 .
.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
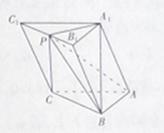

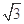 求三棱锥B1-A1DC的体积.
求三棱锥B1-A1DC的体积.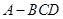 内接于球
内接于球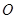 ,且底面边长为
,且底面边长为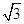 ,侧棱长为2,则球
,侧棱长为2,则球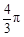
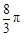
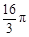
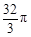
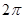 的半圆面,则该圆锥的体积为________.
的半圆面,则该圆锥的体积为________. 中,
中,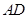 与
与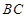 互相垂直,
互相垂直,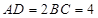 ,且
,且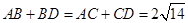 ,则四面体
,则四面体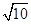
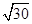
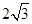 ,底面是等边三角形,则这个三棱锥的体积为( )
,底面是等边三角形,则这个三棱锥的体积为( )