题目内容
在三棱锥 中,
中, ,
, ,
, ,二面角
,二面角 的余弦值是
的余弦值是 ,若
,若 都在同一球面上,则该球的表面积是.
都在同一球面上,则该球的表面积是.
 中,
中, ,
, ,
, ,二面角
,二面角 的余弦值是
的余弦值是 ,若
,若 都在同一球面上,则该球的表面积是.
都在同一球面上,则该球的表面积是. .
.试题分析:取
 中点
中点 ,连接
,连接 ,∵
,∵ ,∴
,∴ ,∵
,∵ ,
,∴
 ,
, 平面
平面 .∴
.∴ 为二面角
为二面角 .在
.在 中,
中, ,
, ,
,∴
 .取等边
.取等边 的中心
的中心 ,作
,作 平面
平面 ,过
,过 作
作 平面
平面 ,
, 为外接球球心,
为外接球球心,∴
 ,二面角
,二面角 的余弦值是
的余弦值是 ,所以
,所以 ,
, ,
,∴
 ,∴
,∴ 点为四面体的外接球球心,其半径为
点为四面体的外接球球心,其半径为 ,表面积为
,表面积为 .
.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
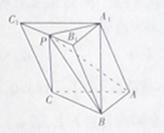
 中,侧棱
中,侧棱 平面
平面 ,
,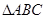 为等腰直角三角形,
为等腰直角三角形, ,且
,且 分别是
分别是 的中点.
的中点.
 平面
平面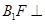 平面
平面 ;
; ,求三棱锥
,求三棱锥 的体积.
的体积. 是边长为6的等边三角形,
是边长为6的等边三角形, 分别为
分别为 靠近
靠近 的三等分点,点
的三等分点,点 为边
为边 边的中点,线段
边的中点,线段 交线段
交线段 于点
于点 .将
.将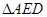 沿
沿 平面
平面 ,连接
,连接 ,形成如图乙所示的几何体.
,形成如图乙所示的几何体.
 平面
平面
 的体积.
的体积.  ,它的三视图中的俯视图如图所示,侧视图是一个矩形,则这个矩形的面积是( )
,它的三视图中的俯视图如图所示,侧视图是一个矩形,则这个矩形的面积是( )

 的正三角形,侧棱垂直于底面,且该三棱柱的外接球表面积为12
的正三角形,侧棱垂直于底面,且该三棱柱的外接球表面积为12 ,则该三棱柱的体积为.
,则该三棱柱的体积为. 中,
中,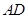 与
与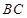 互相垂直,
互相垂直,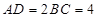 ,且
,且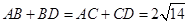 ,则四面体
,则四面体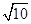
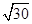
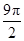 ,则正方体的棱长为 .
,则正方体的棱长为 .