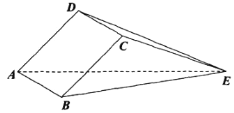
题目内容
【题目】“互倒函数”的定义如下：对于定义域内每一个
，都有
成立，若现在已知函数
是定义域在
的“互倒函数”，且当
时，
成立.若函数
（
）都恰有两个不同的零点，则实数
的取值范围是( )
A.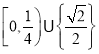
B.
C.
D.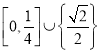
【答案】A
【解析】
根据
是“互倒函数”，得到解析式，从而画出的图像，将问题等价于等价于
有两个不等的实根，分为
，
，
，
，
几种情况讨论，设
，先研究
的解，再研究的解，从而得到
的范围.
函数是定义域在
的“互倒函数”
当
，则
，
因为
，且当
时，
，
所以
，
所以
，
函数
都恰有两个不同的零点，
等价于有两个不等的实根，
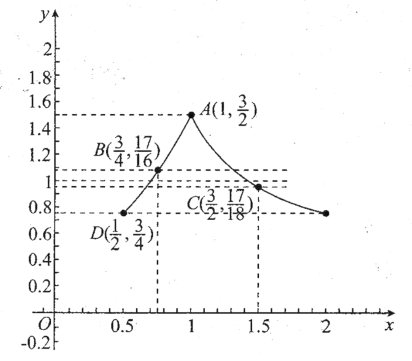
作出的大致图像，如图所示，
可得
，
，
，
.
设，则
①当时，有两个解
，
，
其中
，
，
无解，
有两个解，符合题意；
②当时，由得
，
，
由图可知此时
有四个解，不符合题意；
③当时，有两个解，，
其中
，
，
由图可知此时有四个解，不符合题意；
④当时，由
，得
，
由图可知
有两个解，符合题意；
⑤当时，由，得
无解，不符合题意.
综上所述，或
符合题意，
而
，所以解得
或
.
即实数的取值范围为
.
故选：A.
天天向上一本好卷系列答案
小学生10分钟应用题系列答案【题目】目前，中国有三分之二的城市面临“垃圾围城”的窘境. 我国的垃圾处理多采用填埋的方式，占用上万亩土地，并且严重污染环境. 垃圾分类把不易降解的物质分出来，减轻了土地的严重侵蚀，减少了土地流失. 2020年5月1日起，北京市将实行生活垃圾分类，分类标准为厨余垃圾、可回收物、有害垃圾和其它垃圾四类 .生活垃圾中有30%~40%可以回收利用，分出可回收垃圾既环保，又节约资源. 如：回收利用1吨废纸可再造出0.8吨好纸，可以挽救17棵大树，少用纯碱240千克，降低造纸的污染排放75％，节省造纸能源消耗40％～50％.
现调查了北京市5个小区12月份的生活垃圾投放情况，其中可回收物中废纸和塑料品的投放量如下表：
|
|
|
|
| |
废纸投放量（吨） | 5 | 5.1 | 5.2 | 4.8 | 4.9 |
塑料品投放量（吨） | 3.5 | 3.6 | 3.7 | 3.4 | 3.3 |
（Ⅰ）从
这5个小区中任取1个小区，求该小区12月份的可回收物中，废纸投放量超过5吨且塑料品投放量超过3.5吨的概率；
（Ⅱ）从这5个小区中任取2个小区，记
为12月份投放的废纸可再造好纸超过4吨的小区个数，求的分布列及期望．
【题目】
大学就业部从该大学2018年已就业的大学本科毕业生中随机抽取了100人进行月薪情况的问卷调查，经统计发现，他们的月薪收入在3000元到10000元之间，具体统计数据如表：
月薪（百万） |
|
|
|
|
|
|
|
人数 | 2 | 15 | 20 | 15 | 24 | 10 | 4 |
（1）经统计发现，该大学2018届的大学本科毕业生月薪
（单位：百元）近似地服从正态分布
，其中
近似为样本平均数
（每组数据取区间的中点值）．若落在区间
的左侧，则可认为该大学本科生属“就业不理想”的学生，学校将联系本人，咨询月薪过低的原因，为以后的毕业生就业提供更好的指导意见．现该校2018届大学本科毕业生张茗的月薪为3600元，试判断张茗是否属于“就业不理想”的学生；
（2）①将样本的频率视为总体的概率，若大学领导决定从大学2018届所有本毕业生中任意选取5人前去探访，记这5人中月薪不低于8000元的人数为
，求的数学期望与方差；
②在（1）的条件下，中国移动赞助了大学的这次社会调查活动，并为这次参与调查的大学本科毕业生制定了赠送话费的活动，赠送方式为：月薪低于的获赠两次随机话费，月薪不低于的获赠一次随机话费；每次赠送的话费及对应的概率分别为：
赠送话费（单位：元） | 50 | 100 | 150 |
概率 |
|
|
|
则张茗预期获得的话费为多少元？（结果保留整数）
