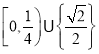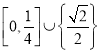题目内容
【题目】如图,四棱锥![]() 中,四边形
中,四边形![]() 是边长为2的菱形,
是边长为2的菱形,![]() ,
,![]() .
.
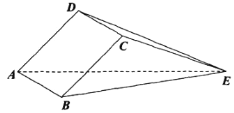
(1)证明:平面![]() 平面
平面![]() ;
;
(2)当直线![]() 与平面
与平面![]() 所成的角为30°时,求平面
所成的角为30°时,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)作![]() ,余弦定理得
,余弦定理得![]() ,在同一平面内用“数据说话”,证
,在同一平面内用“数据说话”,证![]() 用线面垂直的性质可证平面
用线面垂直的性质可证平面![]() 平面
平面![]() ;
;
(2)以![]() 为原点建立空间直角坐标系,使用空间向量求二面角的平面角即可.
为原点建立空间直角坐标系,使用空间向量求二面角的平面角即可.
(1)过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连结
,连结![]() ,
,![]() .
.
在![]() 中,由
中,由![]() ,
,![]() 得,
得,![]() .
.
在![]() 中,由余弦定理得
中,由余弦定理得![]() ,
,
即![]() ,又
,又![]() ,所以
,所以![]() ,即
,即![]() .
.
又![]() ,所以
,所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)由(1)知,![]() 为直线
为直线![]() 与底面
与底面![]() 所成角,则
所成角,则![]() ,所以
,所以![]() .
.
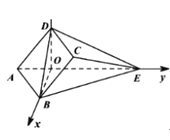
以![]() 为原点,建立空间直角坐标系
为原点,建立空间直角坐标系![]() 如图所示,则
如图所示,则![]() ,
,![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,
,
由于![]() ,所以
,所以![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则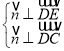 ,即
,即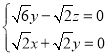 ,解得
,解得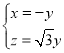 ,
,
令![]() 得
得![]() .
.
显然平面![]() 的一个法向量为
的一个法向量为![]() ,
,
所以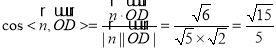 ,
,
即平面![]() 与平面
与平面![]() 所成二面角的余弦值为
所成二面角的余弦值为![]() .
.

练习册系列答案
相关题目
【题目】“互联网![]() ”是“智慧城市”的重要内士,
”是“智慧城市”的重要内士,![]() 市在智慧城市的建设中,为方便市民使用互联网,在主城区覆盖了免费
市在智慧城市的建设中,为方便市民使用互联网,在主城区覆盖了免费![]() .为了解免费
.为了解免费![]() 在
在![]() 市的使用情况,调査机构借助网络进行了问卷调查,并从参与调査的网友中抽取了
市的使用情况,调査机构借助网络进行了问卷调查,并从参与调査的网友中抽取了![]() 人进行抽样分析,得到如下列联表(单位:人):
人进行抽样分析,得到如下列联表(单位:人):
经常使用免费WiFi | 偶尔或不用免费WiFi | 合计 | |
45岁及以下 | 70 | 30 | 100 |
45岁以上 | 60 | 40 | 100 |
合计 | 130 | 70 | 200 |
(1)根据以上数据,判断是否有![]() 的把握认为
的把握认为![]() 市使用免费
市使用免费![]() 的情况与年龄有关;
的情况与年龄有关;
(2)将频率视为概率,现从该市![]() 岁以上的市民中用随机抽样的方法每次抽取
岁以上的市民中用随机抽样的方法每次抽取![]() 人,共抽取
人,共抽取![]() 次.记被抽取的
次.记被抽取的![]() 人中“偶尔或不用免费
人中“偶尔或不用免费![]() ”的人数为
”的人数为![]() ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求![]() 的分布列,数学期望
的分布列,数学期望![]() 和方差
和方差![]() .
.
附: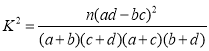 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 |
| 2.072 | 2.706 | 3.841 | 5.024 |