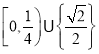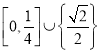题目内容
【题目】数列![]() :
: ![]() 满足:
满足: ![]() .记
.记![]() 的前
的前![]() 项和为
项和为![]() ,并规定
,并规定![]() .定义集合
.定义集合![]() ,
, ![]()
![]() ,
, ![]() .
.
(Ⅰ)对数列![]() :
: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,求集合
,求集合![]() ;
;
(Ⅱ)若集合![]() ,
, ![]() ,证明:
,证明: ![]() ;
;
(Ⅲ)给定正整数![]() .对所有满足
.对所有满足![]() 的数列
的数列![]() ,求集合
,求集合![]() 的元素个数的最小值.
的元素个数的最小值.
【答案】(Ⅰ)![]() .(Ⅱ)见解析;(Ⅲ)
.(Ⅱ)见解析;(Ⅲ)![]() .
.
【解析】
(Ⅰ)根据题中所给的定义,即可求出结果;(Ⅱ)根据所给的条件,由集合![]() 的定义知
的定义知![]() ,再结合
,再结合![]() ,可推出
,可推出![]() ;(Ⅲ)利用(Ⅱ)的结论,进一步求出关系,即集合的最小值.
;(Ⅲ)利用(Ⅱ)的结论,进一步求出关系,即集合的最小值.
(Ⅰ)因为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
所以![]() .
.
(Ⅱ)由集合![]() 的定义知
的定义知![]() ,且
,且![]() 是使得
是使得![]() 成立的最小的k,
成立的最小的k,
所以![]() .
.
又因为 ![]() ,所以
,所以![]() 所以
所以![]() .
.
(Ⅲ)因为![]() ,所以
,所以![]() 非空.
非空.
设集合![]() ,不妨设
,不妨设![]() ,则由(Ⅱ)可知
,则由(Ⅱ)可知![]() ,
,
同理![]() ,且
,且![]() .
.
所以![]()
![]() .
.
因为![]() ,所以
,所以![]() 的元素个数
的元素个数![]() .
.
取常数数列![]() :
: ![]() ,并令
,并令![]() ,则
,则![]() ,适合题意,且
,适合题意,且![]() ,其元素个数恰为
,其元素个数恰为![]() .
.
综上, ![]() 的元素个数的最小值为
的元素个数的最小值为![]() .
.

练习册系列答案
相关题目
【题目】“互联网![]() ”是“智慧城市”的重要内士,
”是“智慧城市”的重要内士,![]() 市在智慧城市的建设中,为方便市民使用互联网,在主城区覆盖了免费
市在智慧城市的建设中,为方便市民使用互联网,在主城区覆盖了免费![]() .为了解免费
.为了解免费![]() 在
在![]() 市的使用情况,调査机构借助网络进行了问卷调查,并从参与调査的网友中抽取了
市的使用情况,调査机构借助网络进行了问卷调查,并从参与调査的网友中抽取了![]() 人进行抽样分析,得到如下列联表(单位:人):
人进行抽样分析,得到如下列联表(单位:人):
经常使用免费WiFi | 偶尔或不用免费WiFi | 合计 | |
45岁及以下 | 70 | 30 | 100 |
45岁以上 | 60 | 40 | 100 |
合计 | 130 | 70 | 200 |
(1)根据以上数据,判断是否有![]() 的把握认为
的把握认为![]() 市使用免费
市使用免费![]() 的情况与年龄有关;
的情况与年龄有关;
(2)将频率视为概率,现从该市![]() 岁以上的市民中用随机抽样的方法每次抽取
岁以上的市民中用随机抽样的方法每次抽取![]() 人,共抽取
人,共抽取![]() 次.记被抽取的
次.记被抽取的![]() 人中“偶尔或不用免费
人中“偶尔或不用免费![]() ”的人数为
”的人数为![]() ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求![]() 的分布列,数学期望
的分布列,数学期望![]() 和方差
和方差![]() .
.
附: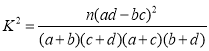 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 |
| 2.072 | 2.706 | 3.841 | 5.024 |