题目内容
【题目】已知向量
,若函数
的最小正周期为
，且在
上单调递减.
(1)求
的解析式；
(2)若关于
的方程
在
有实数解，求
的取值范围.
【答案】(1) 
(2) 
【解析】
（1）利用两角和与差的三角函数化简函数的解析式，求出函数的周期，得到ω，然后求解函数的解析式．
（2）化简方程为：2a（sin2x+cos2x）2﹣2（sin2x﹣cos2x）﹣3a+3=0，令
，原方程化为2a（2﹣t2）﹣2t﹣3a+3=0，整理2at2+2t﹣a﹣3=0，等价于2at2+2t﹣a﹣3=0在[﹣1，1]有解．
(1)
=
，由
当
，此时
在
上单调递增，不符合题意
当
，
，此时在上单调递减，符合题意
所以
(2)方程
即方程
，设
方程等价于在
在
有解
设
当
，若
不符合题意
当
时，
在有解：
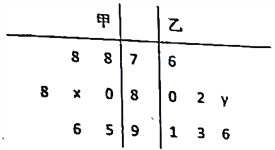
方程在有一解，
方程在在有二解，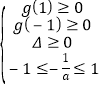
综上所述：
的范围
开心蛙状元测试卷系列答案【题目】某工厂为了对新研发的一种产品进行合理定价，将该产品按事先拟定的价格进行试销，得到如下数据：
单价x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
(1)求回归直线方程
＝bx＋a；（其中
，
，
，
，
）；
(2)预计在今后的销售中，销量与单价仍然服从(1)中的关系，且该产品的成本是4元/件，为使工厂获得最大利润，该产品的单价应定为多少元？(利润＝销售收入－成本)
【题目】某保险公司利用简单随机抽样方法,对投保车辆进行抽样,样本车辆中每辆车的赔付结果统计如下:
赔付金额(元) | 0 | 1 000 | 2 000 | 3 000 | 4 000 |
车辆数(辆) | 500 | 130 | 100 | 150 | 120 |
(1)若每辆车的投保金额均为2800元,估计赔付金额大于投保金额的概率.
(2)在样本车辆中,车主是新司机的占10%,在赔付金额为4000元的样本车辆中,车主是新司机的占20%,估计在已投保车辆中,新司机获赔金额为4000元的概率.