题目内容
某班从6名干部中（其中男生4人，女生2人），选3人参加学校的义务劳动.
（I）设所选3人中女生人数为ξ，求ξ的分布列及Eξ；
（II）求男生甲或女生乙被选中的概率；
（III）在男生甲被选中的情况下，求女生乙也被选中的概率.
（I）设所选3人中女生人数为ξ，求ξ的分布列及Eξ；
（II）求男生甲或女生乙被选中的概率；
（III）在男生甲被选中的情况下，求女生乙也被选中的概率.
（1）1（2） 
（I）ξ的所有可能取值为0，1，2，依题意得：
∴ξ的分布列为
∴Eξ=0×
+1×
+2×=1.
（II）设“甲、乙都不被选中”的事件为C，则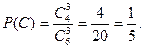
∴所求概率为
（III）记“男生甲被选中”为事件A，“女生乙被选中”为事件B，
∴ξ的分布列为
| ξ | 0 | 1 | 2 |
| P | | | |
+1×+2×=1.（II）设“甲、乙都不被选中”的事件为C，则
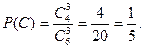
∴所求概率为
（III）记“男生甲被选中”为事件A，“女生乙被选中”为事件B，
练习册系列答案
名校课堂系列答案
相关题目
．
的概率；
的概率P；
，
，
的频率分布直方图中对应的小矩形的高分别是
，问所取的40名学生的成绩不低于
分的共有多少人？
，且互相独立，求电路被接通的概率？
，则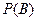
= ．