题目内容
某班委会由4名男生与3名女生组成,现从中选出2人担任正、副班长,其中至少有1名女生当选的概率是___________.
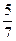
4名男生与3名女生共3人,选1人任正班长有7种选法,再选1人任副班长有6种选法,故共有7×6=42种不同选法(注意“甲任正乙任副”与“乙任正甲任副”是不同的事件).
“至少有1名女生当选”是事件A“恰有1女生和1男生当选”与B“恰有2女生当选”之和.
事件A包含的基本事件数为4×3×2=24,事件B包含的基本事件数为3×2=6,根据概率的加法公式,得P=P(A)+P(B)=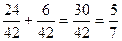 .
.
另解,事件C“至少有1名女生当选”的对立事件是事件D“没有女生当选”,即“两名男生当选”,其基本事件数为4×3=12.事件D的概率是P(D)=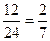 .根据对立事件的概率,则P(C)=1-P(D)=1-
.根据对立事件的概率,则P(C)=1-P(D)=1-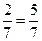 .
.
“至少有1名女生当选”是事件A“恰有1女生和1男生当选”与B“恰有2女生当选”之和.
事件A包含的基本事件数为4×3×2=24,事件B包含的基本事件数为3×2=6,根据概率的加法公式,得P=P(A)+P(B)=
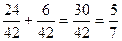 .
.另解,事件C“至少有1名女生当选”的对立事件是事件D“没有女生当选”,即“两名男生当选”,其基本事件数为4×3=12.事件D的概率是P(D)=
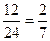 .根据对立事件的概率,则P(C)=1-P(D)=1-
.根据对立事件的概率,则P(C)=1-P(D)=1-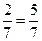 .
.
练习册系列答案
相关题目
 中任取三个,这三点能构成三角形的概率是 (结果用分数表示).
中任取三个,这三点能构成三角形的概率是 (结果用分数表示). ”三类经济型轿车中,每类轿车均有舒适和标准两种型号.某周产量如下表:
”三类经济型轿车中,每类轿车均有舒适和标准两种型号.某周产量如下表:
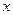
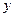
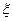 ,求
,求



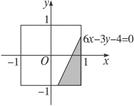
 .
.