题目内容
某校高二年级有学生1000人,在某次数学考试中,为研究学生的考试情况,需从中抽取40名学生的成绩,
(1)问采用何种抽样方法更合适?
(2)根据所抽取的40名学生成绩,分组在 ,
, ,
, 的频率分布直方图中对应的小矩形的高分别是
的频率分布直方图中对应的小矩形的高分别是 ,问所取的40名学生的成绩不低于
,问所取的40名学生的成绩不低于 分的共有多少人?
分的共有多少人?
(3)在(2)所求的成绩不低于 分的学生中任取2人为一组(不分先后),求至少有1人的成绩在
分的学生中任取2人为一组(不分先后),求至少有1人的成绩在 内的概率.
内的概率.
(1)问采用何种抽样方法更合适?
(2)根据所抽取的40名学生成绩,分组在
 ,
, ,
, 的频率分布直方图中对应的小矩形的高分别是
的频率分布直方图中对应的小矩形的高分别是 ,问所取的40名学生的成绩不低于
,问所取的40名学生的成绩不低于 分的共有多少人?
分的共有多少人?(3)在(2)所求的成绩不低于
 分的学生中任取2人为一组(不分先后),求至少有1人的成绩在
分的学生中任取2人为一组(不分先后),求至少有1人的成绩在 内的概率.
内的概率.(1)系统抽样
(2)所取40名学生成绩不低于120分的有8人
(3)至少有1人的成绩在 内的概率为
内的概率为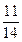
(2)所取40名学生成绩不低于120分的有8人
(3)至少有1人的成绩在
 内的概率为
内的概率为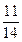
(1)系统抽样方法更合适.
(2)由题意得:在分组 ,
, ,
, 中的学生频率分别是
中的学生频率分别是
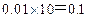 ,
, 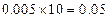 ,
, 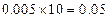 所以所取的40名学生的成绩不低于120分的人数为:
所以所取的40名学生的成绩不低于120分的人数为:
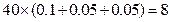 人 (3)由(2)知成绩在
人 (3)由(2)知成绩在 的学生有4人,设编号为1、2、3、4
的学生有4人,设编号为1、2、3、4
成绩在 的学生有2人,设编号为5、6
的学生有2人,设编号为5、6
成绩在 的学生有2人,设编号为7、8
的学生有2人,设编号为7、8
则从这8人中任取2人为一组共有的分组方法为:
(1、2)、(1、3)、(1、4)、(1、5)、(1、6)、(1、7)、(1、8)
(2、3)、(2、4)、(2、5)、(2、6)、(2、7)、(2、8)
(3、4)、(3、5)、(3、6)、(3、7)、(3、8)
(4、5)、(4、6)、(4、7)、(4、8)
(5、6)、(5、7)、(5、8)
(6、7)、(6、8)
(7、8)
共28种分组方法,且是等可能基本事件
记事件A为“至少有1人的成绩在 内”.
内”.
则事件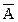 为“2人的成绩均在
为“2人的成绩均在 内”
内”
因为事件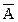 所包含的基本事件有6个,所以:
所包含的基本事件有6个,所以: 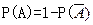 =
= =
=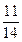 .
.
. 答:(1)系统抽样
(2)所取40名学生成绩不低于120分的有8人
(3)至少有1人的成绩在 内的概率为
内的概率为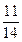
(2)由题意得:在分组
 ,
, ,
, 中的学生频率分别是
中的学生频率分别是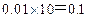 ,
, 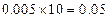 ,
, 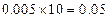 所以所取的40名学生的成绩不低于120分的人数为:
所以所取的40名学生的成绩不低于120分的人数为: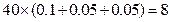 人 (3)由(2)知成绩在
人 (3)由(2)知成绩在 的学生有4人,设编号为1、2、3、4
的学生有4人,设编号为1、2、3、4成绩在
 的学生有2人,设编号为5、6
的学生有2人,设编号为5、6成绩在
 的学生有2人,设编号为7、8
的学生有2人,设编号为7、8 则从这8人中任取2人为一组共有的分组方法为:
(1、2)、(1、3)、(1、4)、(1、5)、(1、6)、(1、7)、(1、8)
(2、3)、(2、4)、(2、5)、(2、6)、(2、7)、(2、8)
(3、4)、(3、5)、(3、6)、(3、7)、(3、8)
(4、5)、(4、6)、(4、7)、(4、8)
(5、6)、(5、7)、(5、8)
(6、7)、(6、8)
(7、8)
共28种分组方法,且是等可能基本事件
记事件A为“至少有1人的成绩在
 内”.
内”.则事件
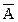 为“2人的成绩均在
为“2人的成绩均在 内”
内”因为事件
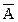 所包含的基本事件有6个,所以:
所包含的基本事件有6个,所以: 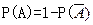 =
= =
=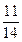 .
. . 答:(1)系统抽样
(2)所取40名学生成绩不低于120分的有8人
(3)至少有1人的成绩在
 内的概率为
内的概率为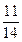

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ”三类经济型轿车中,每类轿车均有舒适和标准两种型号.某周产量如下表:
”三类经济型轿车中,每类轿车均有舒适和标准两种型号.某周产量如下表: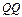
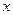
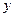
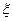 ,求
,求 ,第二次出现的点数记为
,第二次出现的点数记为 ,试就方程组
,试就方程组 解答下列各题:
解答下列各题:


 、
、 是两个随机事件,
是两个随机事件, ,
, ,
, ,则
,则 .
.