题目内容
已知某椭圆的焦点F1(-4,0),F2(4,0),过点F2并垂直于x轴的直线与椭圆的一个交点为B,且|F1B|+|F2B|=10,椭圆上不同两点A(x 1,y1),C(x2,y2)满足条件|F2A|,|F2B|,|F2C|成等差数列.(1)求该椭圆的方程;(2)求弦AC中点的横坐标.
1,y1),C(x2,y2)满足条件|F2A|,|F2B|,|F2C|成等差数列.(1)求该椭圆的方程;(2)求弦AC中点的横坐标.
解:(1 )由椭圆的定义及已知条件知:2a=|F1B|+|F2B|=10,所以a=5,又c=4,故b=3,.故椭圆的方程为
)由椭圆的定义及已知条件知:2a=|F1B|+|F2B|=10,所以a=5,又c=4,故b=3,.故椭圆的方程为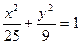 . (4分)
. (4分)
(2)由点B(4,y0)在椭圆上,得|F2B|=|y0|=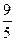 ,因为椭圆的右准线方程为
,因为椭圆的右准线方程为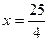 ,
,
离心率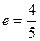 .所以根据椭圆的第二定义,有
.所以根据椭圆的第二定义,有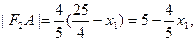
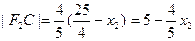 .因为|F2A|,|F2B|,|F2C|成等差数列,
.因为|F2A|,|F2B|,|F2C|成等差数列,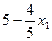 +
+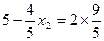 ,所以:x1+x2="8, " 从而弦AC的中点的横坐标为
,所以:x1+x2="8, " 从而弦AC的中点的横坐标为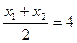 。
。
解析

练习册系列答案
相关题目
22.(本题满分15分)已知抛物线C的顶点在原点,焦点在y轴正半轴上,点 到其准线的距离等于5.
到其准线的距离等于5.
(Ⅰ)求抛物线C的方程;
(Ⅱ)如图,过抛物线C的焦点的直线从左到右依次与抛物线C及圆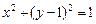 交于A、C、D、B四点,试证明
交于A、C、D、B四点,试证明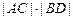 为定值;
为定值;
|
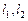 且
且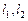 交于点M,求
交于点M,求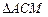 与
与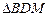 面积之和的最小值.
面积之和的最小值. 将椭圆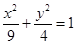 按φ:
按φ: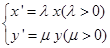 ,变换后得到圆
,变换后得到圆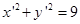 ,则( )
,则( )
| A.λ="3," μ=4 | B.λ="3," μ=2 | C.λ="1," μ=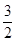 | D.λ="1," μ=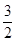 |
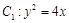 的焦点到准线的距离与椭圆
的焦点到准线的距离与椭圆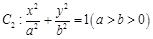 的长半轴相等,设椭圆的右顶点为
的长半轴相等,设椭圆的右顶点为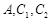 在第一象限的交点为
在第一象限的交点为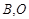 为坐标原点,且
为坐标原点,且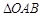 的面积为
的面积为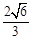
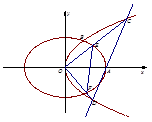
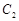 的标准方程;
的标准方程;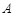 作直线
作直线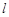 交
交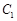 于
于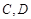 两点,射线
两点,射线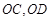 分别交
分别交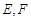 两点.
两点.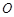 点在以
点在以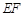 为直径的圆的内部;
为直径的圆的内部;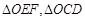 的面积分别为
的面积分别为 ,问是否存在直线
,问是否存在直线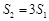 ?请说明理由.
?请说明理由.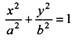 (a〉b>0)的左焦点为
(a〉b>0)的左焦点为 ,椭圆过点P(
,椭圆过点P(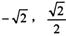 )
) 与椭圆C交于A、B两点,以DA和DB为邻边的四边形是菱形,求k的取值范围.
与椭圆C交于A、B两点,以DA和DB为邻边的四边形是菱形,求k的取值范围.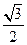 ,求m的值及椭圆的长轴和短轴的长及顶点坐标.
,求m的值及椭圆的长轴和短轴的长及顶点坐标. 圆
圆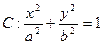 ,
,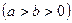 的离心率为
的离心率为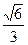 ,直线
,直线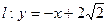 与以
与以 原点为圆心,以椭圆
原点为圆心,以椭圆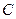 的短半轴长为半径的圆相切。
的短半轴长为半径的圆相切。 、求椭圆
、求椭圆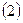 、过点
、过点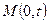 的直线
的直线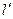 (斜率存在时)与椭圆
(斜率存在时)与椭圆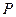 、
、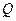 两点,设
两点,设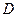 为椭圆
为椭圆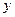 轴负半轴的交点,且
轴负半轴的交点,且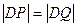 ,求实数
,求实数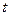 的取值范围。
的取值范围。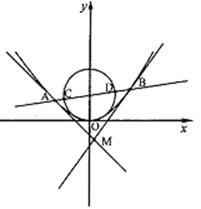
 )的直线l过点(0,-2
)的直线l过点(0,-2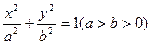
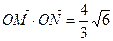 cot∠MON ≠0(O为原点).若存在,求直线m的方程;若不存
cot∠MON ≠0(O为原点).若存在,求直线m的方程;若不存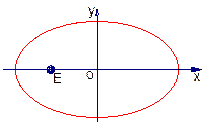
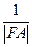 +
+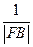 为定值.
为定值.