题目内容
设椭圆C: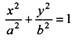 (a〉b>0)的左焦点为
(a〉b>0)的左焦点为 ,椭圆过点P(
,椭圆过点P(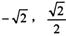 )
)
(1)求椭圆C的方程;
(2)已知点D(l,0),直线l: 与椭圆C交于A、B两点,以DA和DB为邻边的四边形是菱形,求k的取值范围.
与椭圆C交于A、B两点,以DA和DB为邻边的四边形是菱形,求k的取值范围.
解 (1)由题意知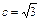 ,b2 = a2-3,由
,b2 = a2-3,由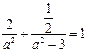 得 2a4-11a2 + 12 = 0,
得 2a4-11a2 + 12 = 0,
所以(a2-4)(2a2-3)= 0,得 a2 = 4或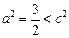 (舍去),
(舍去),
因此椭圆C的方程为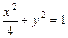 . ……………… 4分
. ……………… 4分
(2)由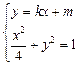 得
得 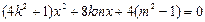 .
.
所以4k2 + 1>0,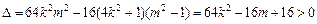 ,
,
得 4k2 + 1>m2. ① ……………… 6分
设A(x1,y1),B(x2,y2),AB中点为M(x0,y0),
则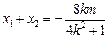 ,
,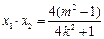 ,
,
于是 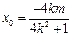 ,
, ,
,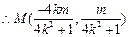 .
.
设菱形一条对角线的方程为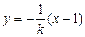 ,则有 x =-ky + 1.
,则有 x =-ky + 1.
将点M的坐标代入,得 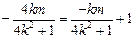 ,所以
,所以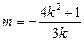 . ②
. ②
将②代入①,得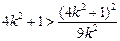 ,
,
所以9k2>4k2 + 1,解得 k∈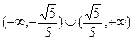 . ……………… 12分
. ……………… 12分
法2: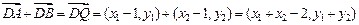
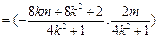
则由菱形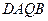 对角线互相垂直,即直线l与
对角线互相垂直,即直线l与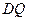 垂直,由斜率的负倒数关系可整理得
垂直,由斜率的负倒数关系可整理得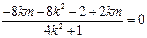 ,即-3km = 4k2 + 1,即
,即-3km = 4k2 + 1,即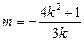 , 代入①即得.
, 代入①即得.
法3: 设A(x1,y1),B(x2,y2),AB中点为M(x0,y0),
则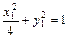 ,
,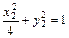 ,于是,两式相减可得
,于是,两式相减可得 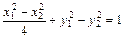 ,
,
即 x0 + 4ky0 = 0. ①
因为 QD⊥AB,所以 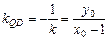 . ②
. ②
由①②可解得 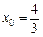 ,
,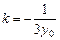 ,表明点M的轨迹为线段
,表明点M的轨迹为线段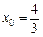 (
(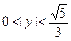 ).
).
当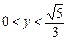 ,k∈(
,k∈(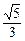 ,+∞);当
,+∞);当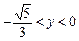 ,k∈(-∞,
,k∈(-∞,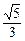 ).
).
综上,k的取值范围是k∈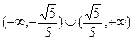 .
.
解析

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
在极坐标系中与圆 相切的一条直线的方程为( )
相切的一条直线的方程为( )
A. | B.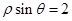 |
C. | D. |
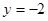 上有一个动点
上有一个动点 ,过点
,过点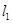 垂直于
垂直于 轴,动点
轴,动点 在
在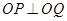 (
(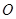 为坐标原点),记点
为坐标原点),记点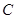 .
.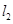 是曲线
是曲线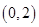 到直线
到直线 的左、右焦点分别为
的左、右焦点分别为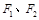 ,上顶点为
,上顶点为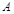 ,离心率为
,离心率为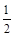 ,在
,在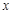 轴负半轴上有一点
轴负半轴上有一点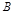 ,且
,且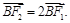
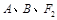 三点的圆恰好与直线
三点的圆恰好与直线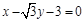 相切,求椭圆C的方程;
相切,求椭圆C的方程;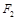 作斜率为
作斜率为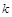 的直线
的直线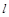 与椭圆C交于
与椭圆C交于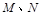 两点,在
两点,在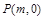 ,使得以
,使得以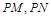 为邻边的平行四边形是菱形?如果存在,求出
为邻边的平行四边形是菱形?如果存在,求出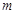 的取值范围;否则,请说明理由.
的取值范围;否则,请说明理由.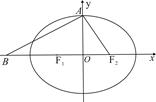
 与抛物线
与抛物线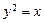 交于
交于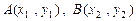 两点,与
两点,与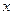 轴相交于点
轴相交于点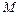 ,且
,且 .
.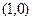 ;
;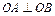 ;
;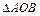 的面积的最小值.
的面积的最小值. ,求△AOB面积的最大值.
,求△AOB面积的最大值.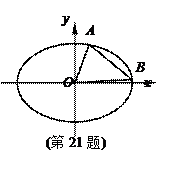
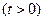 在直线
在直线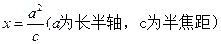 上。
上。 截得的弦长为2的圆的方程;
截得的弦长为2的圆的方程; 1,y1),C(x2,y2)满足条件|F2A|,|F2B|,|F2C|成等差数列.(1)求该椭圆的方程;(2)求弦AC中点的横坐标.
1,y1),C(x2,y2)满足条件|F2A|,|F2B|,|F2C|成等差数列.(1)求该椭圆的方程;(2)求弦AC中点的横坐标.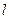 过椭圆
过椭圆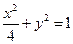 的右焦点,交椭圆于
的右焦点,交椭圆于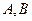 两点,求
两点,求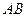 长
长