Question

【题目】设函数，其图象在点处切线的斜率为-3.

（1）求与关系式；

（2）求函数的单调区间（用只含有的式子表示）；

（3）当时，令，设是函数的两个零点， 是与的等差中项，求证： （为函数的导函数）.

Answer 1

【答案】（1）（2）见解析（3）见解析

【解析】试题分析：（1）由导数的几何意义得，即可得解；

（2）由（1）知， ，讨论， 和时导数的正负，从而得函数的单调性；

（3）根据条件得，两式作差得，从而得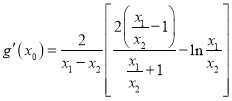， ，构造函数求最值即可证得.

试题解析：

（1）函数的定义域为，

，由得， .

（2）由（1）知， ，

①当时， 在上单调递减；

②当时，令，得，

在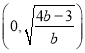上单调递减，在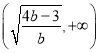上单调递增；

③当时，若时， 在上单调递减；

若时， 在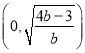上单调递增，在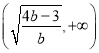上单调递减；

综上，当时， 的单调减区间为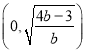，单调增区间为，

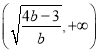当时， 的单调减区间为，

当时， 的单调增区间为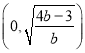，单调减区间为.

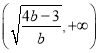（3）当时， ，则， ，

∵与是函数的两个零点，∴，

两式相减得， ，

∵，∴ ，

∵，∴ ，

∴ ，

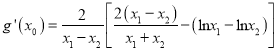
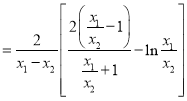令，∵，∴ ， ，

，

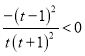∴在单调递减，∴， ，∴ .