题目内容
选修4-2:矩阵与变换(本小题满分10分)
已知矩阵M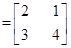
(1) 求矩阵M的逆矩阵;
(2) 求矩阵M的特征值及特征向量;
已知矩阵M
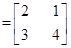
(1) 求矩阵M的逆矩阵;
(2) 求矩阵M的特征值及特征向量;
⑴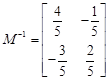 .⑵特征值
.⑵特征值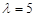 对应的特征向量为
对应的特征向量为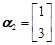 .
.
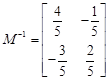 .⑵特征值
.⑵特征值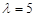 对应的特征向量为
对应的特征向量为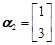 .
.本试题主要考查了逆矩阵的求解,以及矩阵的特征向量和特征值的综合求解运用。根据求解逆矩阵的公式得到第一问,对于第二问中,要对参数进行分类讨论,得到不同情况下的结论。
解:⑴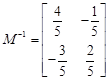 .……………………………………………………………………4分
.……………………………………………………………………4分
⑵ 矩阵A的特征多项式为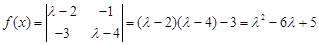 ,
,
令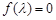 ,得矩阵
,得矩阵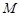 的特征值为
的特征值为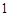 或
或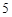 ,…………………………………………6分
,…………………………………………6分
当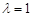 时 由二元一次方程
时 由二元一次方程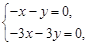 得
得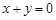 ,令
,令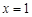 ,则
,则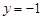 ,
,
所以特征值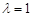 对应的特征向量为
对应的特征向量为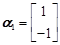 .……………………………………8分
.……………………………………8分
当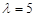 时 由二元一次方程
时 由二元一次方程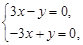 得
得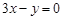 ,令
,令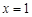 ,则
,则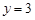 ,
,
所以特征值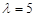 对应的特征向量为
对应的特征向量为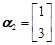 .……………………………………10分
.……………………………………10分
解:⑴
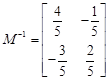 .……………………………………………………………………4分
.……………………………………………………………………4分⑵ 矩阵A的特征多项式为
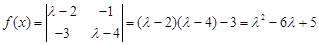 ,
,令
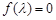 ,得矩阵
,得矩阵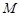 的特征值为
的特征值为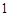 或
或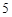 ,…………………………………………6分
,…………………………………………6分当
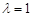 时 由二元一次方程
时 由二元一次方程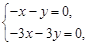 得
得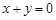 ,令
,令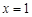 ,则
,则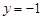 ,
,所以特征值
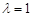 对应的特征向量为
对应的特征向量为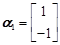 .……………………………………8分
.……………………………………8分当
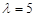 时 由二元一次方程
时 由二元一次方程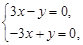 得
得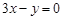 ,令
,令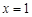 ,则
,则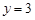 ,
,所以特征值
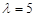 对应的特征向量为
对应的特征向量为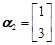 .……………………………………10分
.……………………………………10分
练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
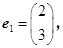 并有特征值λ2=-1及属于特征值-1的一个特征向量
并有特征值λ2=-1及属于特征值-1的一个特征向量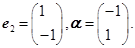 (1)求矩阵M.(2)求M5α.
(1)求矩阵M.(2)求M5α.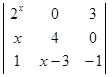 中第1行第3列元素的代数余子式记为
中第1行第3列元素的代数余子式记为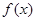 ,则关于
,则关于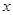 的不等式
的不等式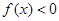 的解集为 .
的解集为 . 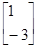 ,属于特征值3的一个特征向量为
,属于特征值3的一个特征向量为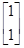 ,求矩阵A.
,求矩阵A.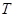 是将平面上每个点
是将平面上每个点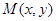 的横坐标乘2,纵坐标乘4,变到点
的横坐标乘2,纵坐标乘4,变到点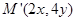 。
。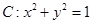 在变换
在变换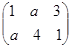 为增广矩阵的线性方程组有唯一一组解,则实数
为增广矩阵的线性方程组有唯一一组解,则实数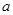 的取值范围为 .
的取值范围为 . 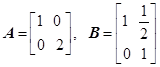 ,若
,若 矩阵
矩阵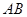 对应的变换把直线
对应的变换把直线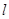 :
: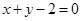 变为
变为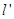 ,求直线
,求直线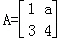 对应的变换将点(﹣2,1)变换成点(0,b),求实数a,b的值.
对应的变换将点(﹣2,1)变换成点(0,b),求实数a,b的值.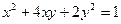 在二阶矩阵
在二阶矩阵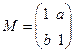 的作用下变换为曲线
的作用下变换为曲线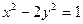
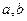 的值;
的值;