题目内容
【题目】一个袋中有2个红球,4个白球.
(1)从中取出3个球,求取到红球个数![]() 的概率分布及数学期望;
的概率分布及数学期望;
(2)每次取1个球,取出后记录颜色并放回袋中.
①若取到第二次红球就停止试验,求第5次取球后试验停止的概率;
②取球4次,求取到红球个数![]() 的概率分布及数学期望.
的概率分布及数学期望.
【答案】(1)分布列见解析,1;(2)①![]() ;②分布列见解析,
;②分布列见解析,![]() .
.
【解析】
(1)利用超几何分布的概率计算公式分别计算出红球个数![]() 的取值为
的取值为![]() 的概率,即可表示分布列,再利用数学期望的计算公式求得对应期望值;
的概率,即可表示分布列,再利用数学期望的计算公式求得对应期望值;
(2)①事件“取到第二次红球就停止试验,第5次取球后试验停止”等价于事件“前4次中恰有一次取出红球,且第5次取出红球”,计算后者独立事件的概率即可;
②利用二项分布的分布计算公式分别计算出红球个数![]() 的取值为
的取值为![]() 的概率,即可表示分布列,再利用数学期望的计算公式求得对应期望值.
的概率,即可表示分布列,再利用数学期望的计算公式求得对应期望值.
(1)取到红球个数![]() 的可能取值为
的可能取值为![]()
所以![]() ,
,![]() ,
,![]() ,
,
即分布列为:
X | 0 | 1 | 2 |
P |
|
|
|
故数学期望为:![]() ;
;
(2)设“取一次取出红球”为事件A,“取一次取出白球”为事件B,且![]() ,
,
①事件“前4次中恰有一次取出红球”记为C,且与“第5次取出红球”相互独立
则若取到第二次红球就停止试验,第5次取球后试验停止的概率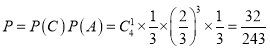
②取球4次,求取到红球个数![]() 的可能取值为
的可能取值为![]()
所以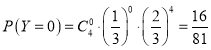 ,
,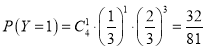 ,
,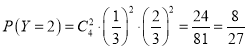 ,
,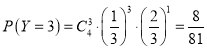 ,
,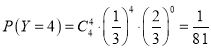
即分布列为:
Y | 0 | 1 | 2 | 3 | 4 |
P |
|
|
|
|
|
故数学期望为:![]()

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
【题目】某医院用光电比色计检查尿汞时,得尿汞含量(毫克/升)与消光系数如下表:
尿汞含量 | 2 | 4 | 6 | 8 | 10 |
消光系数 | 64 | 138 | 205 | 285 | 360 |
(1)作散点图;
(2)如果![]() 与
与![]() 之间具有线性相关关系,求回归线直线方程;
之间具有线性相关关系,求回归线直线方程;
(3)估计尿汞含量为9毫克/升时消光系数.
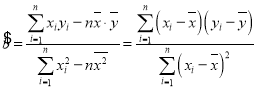 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.