题目内容
【题目】(1)在![]() 中,角A,B,C所对的边分别是a,b,c,证明余弦定理:
中,角A,B,C所对的边分别是a,b,c,证明余弦定理:![]() ;
;
(2)长江某地南北岸平行,如图所示,江面宽度![]() ,一艘游船从南岸码头A出发航行到北岸,假设游船在静水中的航行速度
,一艘游船从南岸码头A出发航行到北岸,假设游船在静水中的航行速度![]() ,水流速度
,水流速度![]() ,设
,设![]() 和
和![]() 的夹角为θ(
的夹角为θ(![]() ),北岸的点
),北岸的点![]() 在点A的正北方向.
在点A的正北方向.
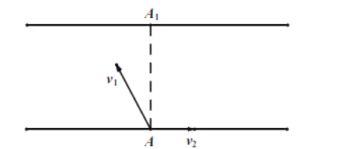
①当![]() 多大时,游船能到达
多大时,游船能到达![]() 处,需要航行多少时间?
处,需要航行多少时间?
②当![]() 时,判断游船航行到达北岸的位置在
时,判断游船航行到达北岸的位置在![]() 的左侧还是右侧,并说明理由.
的左侧还是右侧,并说明理由.
【答案】(1)证明见解析;(2)①![]() 时,需要航行
时,需要航行![]() ;②左侧,理由见解析
;②左侧,理由见解析
【解析】
(1)利用![]() ,两边平方即可证明;
,两边平方即可证明;
(2)①游船能到![]() 处,则游船在水平方向上的速度和水流速度大小相等,得到
处,则游船在水平方向上的速度和水流速度大小相等,得到![]() ,从而解出
,从而解出![]() ,再解出游船垂直江岸方向的速度,即可求得所需时间;②判断游船水平方向上速度向左,即可判断游船到达
,再解出游船垂直江岸方向的速度,即可求得所需时间;②判断游船水平方向上速度向左,即可判断游船到达![]() 的左侧.
的左侧.
(1)利用向量法证明余弦定理:
在![]() 中,
中,![]() ,
,
两边平方可得:![]() ,
,
即![]() ,
,
余弦定理得证;
(2)①若游船能到![]() 处,则游船在水平方向上的速度和水流速度大小相等,
处,则游船在水平方向上的速度和水流速度大小相等,
则有![]() ,得
,得![]() ,
,
所以![]() ,
,
因为![]() ,所以
,所以![]() ,
,
此时游船垂直江岸方向的速度![]() ,
,
时间![]() ,
,
即当![]() 时,游船能到达
时,游船能到达![]() 处,需要航行
处,需要航行![]() ;
;
②![]() 时,游船水平方向的速度大小为
时,游船水平方向的速度大小为![]() ,
,
方向水平向左,故最终到达北岸时游船在![]() 点的左侧.
点的左侧.

 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案【题目】某校共有学生2000人,其中男生1100人,女生900人为了调查该校学生每周平均课外阅读时间,采用分层抽样的方法收集该校100名学生每周平均课外阅读时间(单位:小时)
(1)应抽查男生与女生各多少人?
(2)如图,根据收集100人的样本数据,得到学生每周平均课外阅读时间的频率分布直方图,其中样本数据分组区间为![]() .若在样本数据中有38名女学生平均每周课外阅读时间超过2小时,请完成每周平均课外阅读时间与性别的列联表,并判断是否有95%的把握认为“该校学生的每周平均课外阅读时间与性别有关”.
.若在样本数据中有38名女学生平均每周课外阅读时间超过2小时,请完成每周平均课外阅读时间与性别的列联表,并判断是否有95%的把握认为“该校学生的每周平均课外阅读时间与性别有关”.

男生 | 女生 | 总计 | |
每周平均课外阅读时间不超过2小时 | |||
每周平均课外阅读时间超过2小时 | |||
总计 |
附: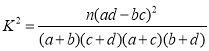
| 0.100 | 0.050 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |

