题目内容
15.若函数f(x)=$\left\{\begin{array}{l}{x-2,x≥2}\\{\frac{1}{2}x-1,x<2}\end{array}\right.$,g(x)=log3x,则函数F(x)=f(x)-g(x)有( )个零点.| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
分析 函数F(x)=f(x)-g(x)零点的个数等于函数f(x),g(x)图象交点的个数,在同一坐标系内画出函数f(x),g(x)图象,数形结合可得答案.
解答 解:函数F(x)=f(x)-g(x)零点的个数等于函数f(x),g(x)图象交点的个数,
在同一坐标系内画出函数f(x),g(x)图象如图所示: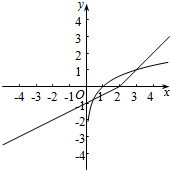
由图可得:函数f(x),g(x)图象共有2个交点,
则函数F(x)=f(x)-g(x)有2个零点.
故选:B
点评 本题考查的知识点是分段函数的应用,函数的零点,难度中档.

练习册系列答案
相关题目
3.方程x2+y2+x+y-m=0表示一个圆,则m的取值范围是( )
| A. | (-$\frac{1}{2}$,+∞) | B. | (-∞,-$\frac{1}{2}$) | C. | (-∞,-$\frac{1}{2}$] | D. | [-$\frac{1}{2}$,+∞) |
4.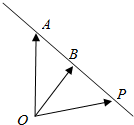 如图,设一条直线上三点A,B,P满足$\overrightarrow{AP}$=λ$\overrightarrow{PB}$(λ≠-1),O是平面上任意一点,则( )
如图,设一条直线上三点A,B,P满足$\overrightarrow{AP}$=λ$\overrightarrow{PB}$(λ≠-1),O是平面上任意一点,则( )
 如图,设一条直线上三点A,B,P满足$\overrightarrow{AP}$=λ$\overrightarrow{PB}$(λ≠-1),O是平面上任意一点,则( )
如图,设一条直线上三点A,B,P满足$\overrightarrow{AP}$=λ$\overrightarrow{PB}$(λ≠-1),O是平面上任意一点,则( )| A. | $\overrightarrow{OP}$=$\frac{\overrightarrow{OA}+λ\overrightarrow{OB}}{1+λ}$(λ≠-1) | B. | $\overrightarrow{OP}$=$\frac{\overrightarrow{OA}+λ\overrightarrow{OB}}{1-λ}$ | ||
| C. | $\overrightarrow{OP}$=$\frac{\overrightarrow{OA}-λ\overrightarrow{OB}}{1+λ}$(λ≠-1) | D. | $\overrightarrow{OP}$=$\frac{\overrightarrow{OA}-2λ\overrightarrow{OB}}{1-λ}$ |
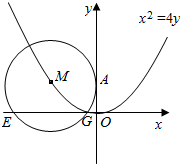 设圆M过点A(0,2),且圆心M在曲线C:x2=4y上,EG是圆M在x轴上截得的弦,试探究当M运动时.弦长|EG|是否为定值?为什么?
设圆M过点A(0,2),且圆心M在曲线C:x2=4y上,EG是圆M在x轴上截得的弦,试探究当M运动时.弦长|EG|是否为定值?为什么?