题目内容
【题目】已知椭圆![]() :
:![]() (
(![]() ),点
),点![]() 是
是![]() 的左顶点,点
的左顶点,点![]() 为
为![]() 上一点,离心率
上一点,离心率![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设过点![]() 的直线
的直线![]() 与
与![]() 的另一个交点为
的另一个交点为![]() (异于点
(异于点![]() ),是否存在直线
),是否存在直线![]() ,使得以
,使得以![]() 为直径的圆经过点
为直径的圆经过点![]() ,若存在,求出直线
,若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
【答案】(1)![]() ;(2)存在,
;(2)存在,![]()
【解析】
(1)把点![]() 代入椭圆C的方程,再结合离心率,可得a,b,c的关系,可得椭圆的方程;
代入椭圆C的方程,再结合离心率,可得a,b,c的关系,可得椭圆的方程;
(2)设出直线![]() 的方程,代入椭圆,运用韦达定理可求得点
的方程,代入椭圆,运用韦达定理可求得点![]() 的坐标,再由
的坐标,再由![]() ,可求得直线的方程,要注意检验直线是否和椭圆有两个交点.
,可求得直线的方程,要注意检验直线是否和椭圆有两个交点.
(1)由题可得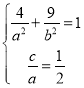 ∴
∴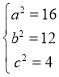 ,所以椭圆
,所以椭圆![]() 的方程
的方程![]()
(2)由题知![]() ,设
,设![]() ,直线
,直线![]() 的斜率存在设为
的斜率存在设为![]() ,
,
则![]() 与椭圆
与椭圆![]() 联立得
联立得![]()
![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,∴
,∴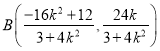
若以![]() 为直径的圆经过点
为直径的圆经过点![]() ,
,
则![]() ,∴
,∴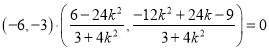 ,
,
化简得![]() ,∴
,∴![]() ,解得
,解得![]() 或
或![]()
因为![]() 与
与![]() 不重合,所以
不重合,所以![]() 舍.
舍.
所以直线![]() 的方程为
的方程为![]() .
.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目