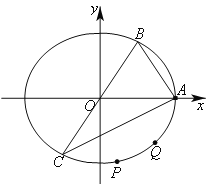
题目内容
【题目】已知![]() 分别是椭圆
分别是椭圆![]() 的左焦点和右焦点,椭圆
的左焦点和右焦点,椭圆![]() 的离心率为
的离心率为![]()
![]() 是椭圆
是椭圆![]() 上两点,点
上两点,点![]() 满足
满足![]() .
.
(1)求![]() 的方程;
的方程;
(2)若点![]() 在圆
在圆![]() 上,点
上,点![]() 为坐标原点,求
为坐标原点,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据焦点坐标和离心率,结合椭圆中![]() 的关系,即可求得
的关系,即可求得![]() 的值,进而得椭圆的标准方程.
的值,进而得椭圆的标准方程.
(2)设出直线![]() 的方程为
的方程为![]() ,由题意可知
,由题意可知![]() 为
为![]() 中点.联立直线与椭圆方程,由韦达定理表示出
中点.联立直线与椭圆方程,由韦达定理表示出![]() ,由判别式
,由判别式![]() 可得
可得![]() ;由平面向量的线性运算及数量积定义,化简
;由平面向量的线性运算及数量积定义,化简![]() 可得
可得![]() ,代入弦长公式化简;由中点坐标公式可得点
,代入弦长公式化简;由中点坐标公式可得点![]() 的坐标,代入圆的方程
的坐标,代入圆的方程![]() ,化简可得
,化简可得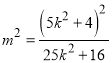 ,代入数量积公式并化简,由换元法令
,代入数量积公式并化简,由换元法令![]() ,代入可得
,代入可得![]() ,再令
,再令![]() 及
及![]() ,结合函数单调性即可确定
,结合函数单调性即可确定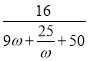 的取值范围,即确定
的取值范围,即确定![]() 的取值范围,因而可得
的取值范围,因而可得![]() 的取值范围.
的取值范围.
(1)![]() 分别是椭圆
分别是椭圆![]() 的左焦点和右焦点,
的左焦点和右焦点,
则![]() ,椭圆
,椭圆![]() 的离心率为
的离心率为![]()
则![]() 解得
解得![]() ,
,
所以![]() ,
,
所以![]() 的方程为
的方程为![]() .
.
(2)设直线![]() 的方程为
的方程为![]() ,点
,点![]() 满足
满足![]() ,则
,则![]() 为
为![]() 中点,点
中点,点![]() 在圆
在圆![]() 上,设
上,设![]() ,
,
联立直线与椭圆方程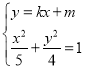 ,化简可得
,化简可得![]() ,
,
所以![]()
则![]() ,化简可得
,化简可得![]() ,
,
而![]()
![]()
![]()
![]()
由弦长公式代入可得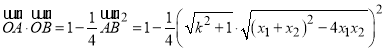
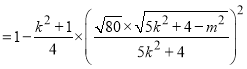
![]() 为
为![]() 中点,则
中点,则![]()
点![]() 在圆
在圆![]() 上,代入化简可得
上,代入化简可得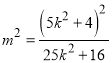 ,
,
所以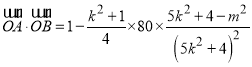
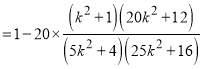
令![]() ,则
,则![]() ,
,![]() ,
,
令![]() ,则
,则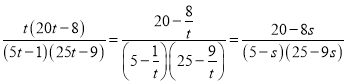
![]()
令![]() ,则
,则![]() ,
,
所以 ,
,
因为![]() 在
在![]() 内单调递增,所以
内单调递增,所以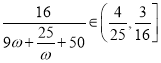 ,
,
即![]()
所以![]()

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目