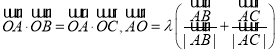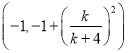题目内容
【题目】正方体![]() 中,
中,![]() 是棱
是棱![]() 的中点,
的中点,![]() 是侧面
是侧面![]() 上的动点,且
上的动点,且![]() 平面
平面![]() ,记
,记![]() 与
与![]() 的轨迹构成的平面为
的轨迹构成的平面为![]() .
.
①![]() ,使得
,使得![]() ;
;
②直线![]() 与直线
与直线![]() 所成角的正切值的取值范围是
所成角的正切值的取值范围是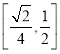 ;
;
③![]() 与平面
与平面![]() 所成锐二面角的正切值为
所成锐二面角的正切值为![]() ;
;
④正方体![]() 的各个侧面中,与
的各个侧面中,与![]() 所成的锐二面角相等的侧面共四个.
所成的锐二面角相等的侧面共四个.
其中正确命题的序号是________.(写出所有正确命题的序号)
【答案】①②③④
【解析】
取![]() 中点
中点![]() ,
,![]() 中点
中点![]() ,
,![]() 中点
中点![]() ,先利用中位线的性质判断点
,先利用中位线的性质判断点![]() 的运动轨迹为线段
的运动轨迹为线段![]() ,平面
,平面![]() 即为平面
即为平面![]() ,画出图形,再依次判断:①利用等腰三角形的性质即可判断;②直线
,画出图形,再依次判断:①利用等腰三角形的性质即可判断;②直线![]() 与直线
与直线![]() 所成角即为直线
所成角即为直线![]() 与直线
与直线![]() 所成角,设正方体的棱长为2,进而求解;③由
所成角,设正方体的棱长为2,进而求解;③由![]() ,取
,取![]() 为
为![]() 中点,则
中点,则![]() ,则
,则![]() 即为
即为![]() 与平面
与平面![]() 所成的锐二面角,进而求解;④由平行的性质及图形判断即可.
所成的锐二面角,进而求解;④由平行的性质及图形判断即可.
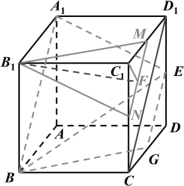
取![]() 中点
中点![]() ,连接
,连接![]() ,则
,则![]() ,所以
,所以![]() ,所以平面
,所以平面![]() 即为平面
即为平面![]() ,
,
取![]() 中点
中点![]() ,
,![]() 中点
中点![]() ,连接
,连接![]() ,则易证得
,则易证得![]() ,
,
所以平面![]() 平面
平面![]() ,所以点
,所以点![]() 的运动轨迹为线段
的运动轨迹为线段![]() ,平面
,平面![]() 即为平面
即为平面![]() .
.
①取![]() 为
为![]() 中点,因为
中点,因为![]() 是等腰三角形,所以
是等腰三角形,所以![]() ,又因为
,又因为![]() ,所以
,所以![]() ,故①正确;
,故①正确;
②直线![]() 与直线
与直线![]() 所成角即为直线
所成角即为直线![]() 与直线
与直线![]() 所成角,设正方体的棱长为2,当点
所成角,设正方体的棱长为2,当点![]() 为
为![]() 中点时,直线
中点时,直线![]() 与直线
与直线![]() 所成角最小,此时
所成角最小,此时![]() ,
,![]() ;
;
当点![]() 与点
与点![]() 或点
或点![]() 重合时,直线
重合时,直线![]() 与直线
与直线![]() 所成角最大,此时
所成角最大,此时![]() ,
,
所以直线![]() 与直线
与直线![]() 所成角的正切值的取值范围是
所成角的正切值的取值范围是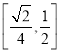 ,②正确;
,②正确;
③![]() 与平面
与平面![]() 的交线为
的交线为![]() ,且
,且![]() ,取
,取![]() 为
为![]() 中点,则
中点,则![]() 即为
即为![]() 与平面
与平面![]() 所成的锐二面角,
所成的锐二面角,![]() ,所以③正确;
,所以③正确;
④正方体![]() 的各个侧面中,平面
的各个侧面中,平面![]() ,平面
,平面![]() ,平面
,平面![]() ,平面
,平面![]() 与平面
与平面![]() 所成的角相等,所以④正确.
所成的角相等,所以④正确.
故答案为:①②③④

【题目】随着手机的发展,“微信”逐渐成为人们交流的一种形式.某机构对“使用微信交流”的态度进行调查,随机抽取了50人,他们年龄的频数分布及对“使用微信交流”赞成人数如下表.
年龄 (单位:岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
(1)若以“年龄45岁为分界点”,由以上统计数据完成下面2×2列联表,并判断是否有99%的把握认为“使用微信交流”的态度与人的年龄有关;
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(2)若从年龄在[55,65)的被调查人中随机选取2人进行追踪调查,求2人中至少有1人不赞成“使用微信交流”的概率.
参考数据:
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
K2=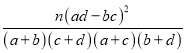 ,其中n=a+b+c+d.
,其中n=a+b+c+d.