题目内容
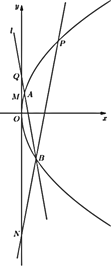
【题目】如图,已知抛物线![]() 经过点
经过点![]() ,过点
,过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 有两个不同的交点
有两个不同的交点![]() 、
、![]() .
.
(1)求直线![]() 的斜率的取值范围;
的斜率的取值范围;
(2)设![]() 为原点,直线
为原点,直线![]() 交
交![]() 轴于
轴于![]() ,直线
,直线![]() 交
交![]() 轴于
轴于![]() ,
,![]() ,
,![]() ,求证:
,求证:![]() 为定值.
为定值.
【答案】(1)![]() ;(2)
;(2)![]() 为定值2,理由见解析.
为定值2,理由见解析.
【解析】
(1)将点P代入抛物线方程,即可求得p的值,设直线AB的方程,代入抛物线方程,由△>0,排除特殊情况,即可求得k的取值范围;
(2)根据向量的共线定理即可求得λ=1﹣yM,μ=1﹣yN,求得直线PA的方程,令x=0,求得M点坐标,同理求得N点坐标,根据韦达定理和向量的坐标表示,即可求得λ+μ为定值.
(1)抛物线C:y2=2px经过点P(1,2),∴4=2p,解得p=2,
根据题意得过点(0,1)的直线斜率存在,设方程为y=kx+1,A(x1,y1),B(x2,y2);
联立方程,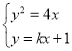 ,可得k2x2+(2k﹣4)x+1=0,
,可得k2x2+(2k﹣4)x+1=0,
∴△=(2k﹣4)2﹣4k2>0,且k≠0解得k<1,
故直线l的斜率的取值范围(﹣∞,0)∪(0,1);
(2)设点M(0,yM),N(0,yN),则 ![]() (0,1﹣yM),
(0,1﹣yM),![]() (0,1);
(0,1);
因为![]() λ
λ![]() ,所以1=λ(1﹣yM),故λ
,所以1=λ(1﹣yM),故λ![]() ,同理μ
,同理μ![]() ,
,
直线PA的方程为y﹣2![]() (x﹣1)
(x﹣1)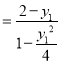 (x﹣1)
(x﹣1)![]() (x﹣1),
(x﹣1),
令x=0,得yM![]() ,同理可得yN
,同理可得yN![]() ,
,
因为λ+μ![]()
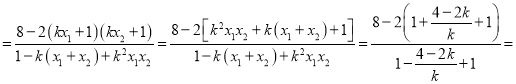 2,
2,
即有λ+μ为定值2.

 阅读快车系列答案
阅读快车系列答案【题目】某班主任对全班50名学生进行了作业量多少的调查,喜欢玩电脑游戏的同学认为作业多的有18人,认为作业不多的有9人,不喜欢玩电脑游戏的同学认为作业多的有8人,认为作业不多的有15人,则认为喜欢玩电脑游戏与认为作业量的多少有关系的把握大约是多少?
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】为考查某种疫苗预防疾病的效果,进行动物实验,得到统计数据如下:
未发病 | 发病 | 总计 | |
未注射疫苗 | 20 |
|
|
注射疫苗 | 30 |
|
|
总计 | 50 | 50 | 100 |
现从所有试验动物中任取一只,取到“注射疫苗”动物的概率为![]() .
.
(1)求![]() 列联表中的数据
列联表中的数据![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)判断疫苗是否有效?
(3)能够有多大把握认为疫苗有效?
(参考公式![]() ,
,![]() )
)
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |