题目内容
给出下列三个命题:①若直线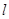 过抛物线
过抛物线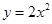 的焦点,且与这条抛物线交于
的焦点,且与这条抛物线交于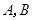 两点,则
两点,则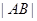 的最小值为
的最小值为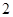 ;②双曲线
;②双曲线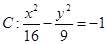 的离心率为
的离心率为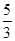 ;③若
;③若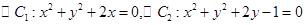 ,则这两圆恰有
,则这两圆恰有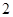 条公切线.④若直线
条公切线.④若直线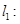
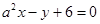 与直线
与直线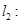
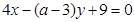 互相垂直,则
互相垂直,则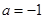 .
.
其中正确命题的序号是 .(把你认为正确命题的序号都填上)
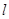 过抛物线
过抛物线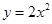 的焦点,且与这条抛物线交于
的焦点,且与这条抛物线交于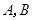 两点,则
两点,则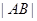 的最小值为
的最小值为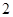 ;②双曲线
;②双曲线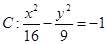 的离心率为
的离心率为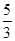 ;③若
;③若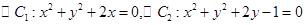 ,则这两圆恰有
,则这两圆恰有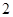 条公切线.④若直线
条公切线.④若直线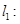
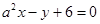 与直线
与直线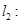
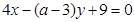 互相垂直,则
互相垂直,则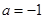 .
.其中正确命题的序号是 .(把你认为正确命题的序号都填上)
②③
:
解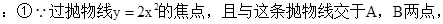
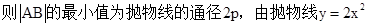
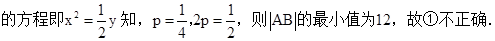
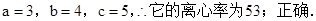

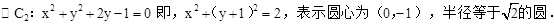
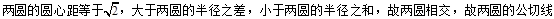
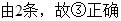

故答案为:②③.
解
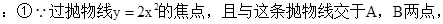
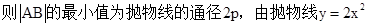
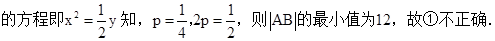
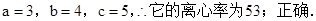

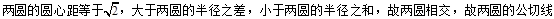
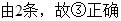

故答案为:②③.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
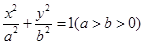 的左、右顶点分别为
的左、右顶点分别为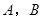 ,点
,点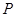 在椭圆上且异于
在椭圆上且异于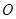 为坐标原点.
为坐标原点.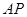 与
与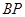 的斜率之积为
的斜率之积为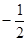 ,求椭圆的离心率;
,求椭圆的离心率;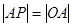 ,证明直线
,证明直线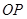 的斜率
的斜率 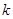 满足
满足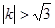
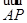 ·
·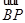 =k|
=k|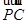 |2.
|2.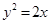 上的两点A、B到焦点的距离和是5,则线段AB的中点到
上的两点A、B到焦点的距离和是5,则线段AB的中点到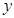 轴的距离为( )
轴的距离为( )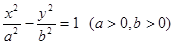 的离心率
的离心率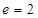 ,右焦点
,右焦点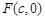 ,方程
,方程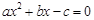 的两个根分别为
的两个根分别为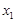 ,
,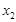 ,则点
,则点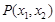 在
在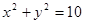 内
内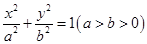 的左、右焦点分别为
的左、右焦点分别为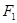 ,
,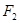 , 点
, 点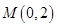 是椭圆的一个顶点,△
是椭圆的一个顶点,△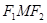 是等腰直角三角形.
是等腰直角三角形.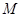 分别作直线
分别作直线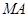 ,
,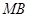 交椭圆于
交椭圆于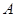 ,
,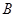 两点,设两直线的斜率分别为
两点,设两直线的斜率分别为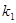 ,
,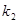 ,且
,且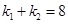 ,证明:直线
,证明:直线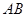 过定点(
过定点(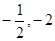 ).
).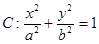 经过点(0,
经过点(0,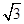 ),离心率为
),离心率为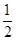 ,直线l经过椭圆C的右焦点F交
,直线l经过椭圆C的右焦点F交 椭圆于A、B两点,点A、F、B在直线x=4上的射影依次为点D、K、E.
椭圆于A、B两点,点A、F、B在直线x=4上的射影依次为点D、K、E.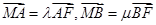 ,当直线l的倾斜角变化时,探求
,当直线l的倾斜角变化时,探求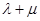 的值是否为定值?若是,求出
的值是否为定值?若是,求出
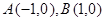 ,
,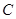 为平面内一动点,且满足
为平面内一动点,且满足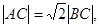 那么点
那么点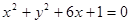
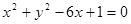
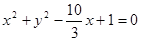

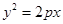 的准线与双曲线
的准线与双曲线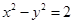 的左准线重合,则p的值为 ▲
的左准线重合,则p的值为 ▲