题目内容
已知椭圆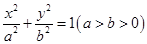 的左、右焦点分别为
的左、右焦点分别为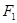 ,
,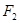 , 点
, 点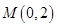 是椭圆的一个顶点,△
是椭圆的一个顶点,△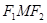 是等腰直角三角形.
是等腰直角三角形.
(Ⅰ)求椭圆的方程;
(Ⅱ)过点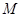 分别作直线
分别作直线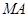 ,
,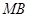 交椭圆于
交椭圆于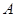 ,
,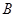 两点,设两直线的斜率分别为
两点,设两直线的斜率分别为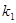 ,
,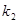 ,且
,且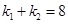 ,证明:直线
,证明:直线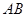 过定点(
过定点(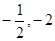 ).
).
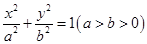 的左、右焦点分别为
的左、右焦点分别为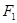 ,
,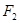 , 点
, 点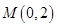 是椭圆的一个顶点,△
是椭圆的一个顶点,△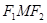 是等腰直角三角形.
是等腰直角三角形.(Ⅰ)求椭圆的方程;
(Ⅱ)过点
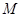 分别作直线
分别作直线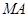 ,
,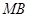 交椭圆于
交椭圆于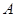 ,
,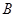 两点,设两直线的斜率分别为
两点,设两直线的斜率分别为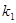 ,
,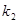 ,且
,且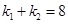 ,证明:直线
,证明:直线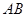 过定点(
过定点(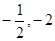 ).
).(Ⅰ)由已知可得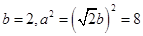 ,
,
所求椭圆方程为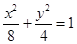 . ……4分
. ……4分
(Ⅱ)若直线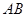 的斜率存在,设
的斜率存在,设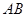 方程为
方程为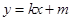 ,依题意
,依题意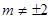 .
.
设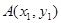 ,
,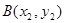 ,
,
由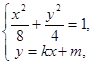 得
得 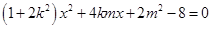 . ……6分
. ……6分
则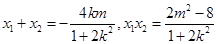 . 由已知
. 由已知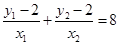 ,
,
所以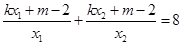 ,即
,即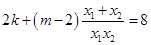 . ……8分
. ……8分
所以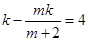 ,整理得
,整理得 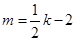 .
.
故直线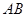 的方程为
的方程为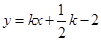 ,即
,即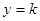 (
(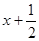 )
)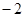 .
.
所以直线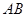 过定点(
过定点(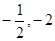 ). ………10分
). ………10分
若直线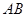 的斜率不存在,设
的斜率不存在,设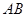 方程为
方程为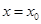 ,
,
设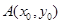 ,
,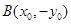 ,由已知
,由已知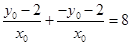 ,
,
得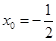 .此时
.此时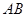 方程为
方程为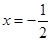 ,显然过点(
,显然过点(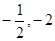 ).
).
综上,直线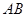 过定点(
过定点(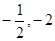 ).
).
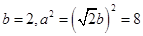 ,
,所求椭圆方程为
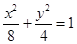 . ……4分
. ……4分(Ⅱ)若直线
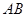 的斜率存在,设
的斜率存在,设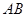 方程为
方程为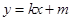 ,依题意
,依题意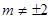 .
.设
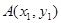 ,
,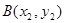 ,
,由
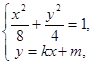 得
得 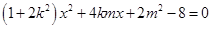 . ……6分
. ……6分则
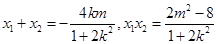 . 由已知
. 由已知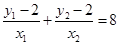 ,
,所以
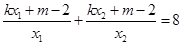 ,即
,即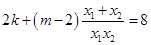 . ……8分
. ……8分所以
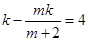 ,整理得
,整理得 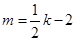 .
.故直线
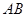 的方程为
的方程为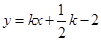 ,即
,即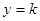 (
(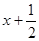 )
)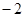 .
.所以直线
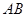 过定点(
过定点(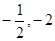 ). ………10分
). ………10分若直线
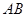 的斜率不存在,设
的斜率不存在,设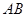 方程为
方程为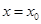 ,
,设
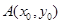 ,
,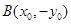 ,由已知
,由已知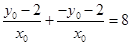 ,
,得
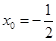 .此时
.此时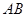 方程为
方程为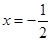 ,显然过点(
,显然过点(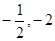 ).
).综上,直线
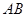 过定点(
过定点(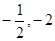 ).
).略

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
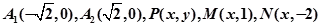 ,若实数
,若实数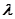 使得
使得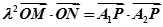 (
(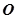 为坐标原点)
为坐标原点)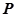 点的轨迹方程,并讨论
点的轨迹方程,并讨论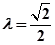 时,若过点
时,若过点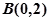 的直线与(1)中
的直线与(1)中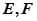 (
(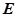 在
在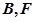 之间),试求
之间),试求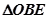 与
与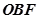 面积之比的取值范围。
面积之比的取值范围。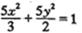
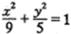
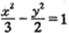

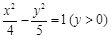
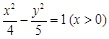
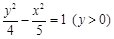
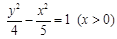
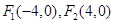 又
又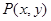 是曲线
是曲线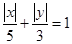 上的点,则( )
上的点,则( )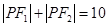
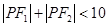
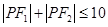
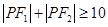
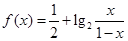 的图象上任两点,且
的图象上任两点,且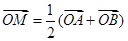 ,已知点M横坐标为
,已知点M横坐标为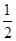 ,
,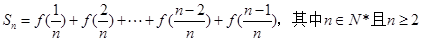 ,求Sn。
,求Sn。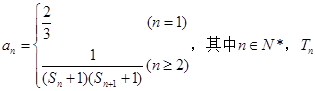 为数列{an}的前n项和, 若
为数列{an}的前n项和, 若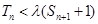 对一切
对一切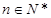 都成立,求
都成立,求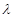 取值范围。
取值范围。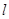 过抛物线
过抛物线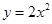 的焦点,且与这条抛物线交于
的焦点,且与这条抛物线交于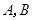 两点,则
两点,则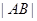 的最小值为
的最小值为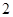 ;②双曲线
;②双曲线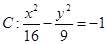 的离心率为
的离心率为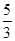 ;③若
;③若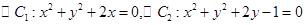 ,则这两圆恰有
,则这两圆恰有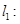
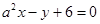 与直线
与直线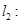
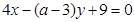 互相垂直,则
互相垂直,则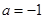 .
.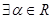 ,使得
,使得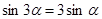 ; ②
; ②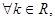 曲线
曲线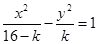 表示双曲线;
表示双曲线;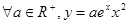 的递减区间为
的递减区间为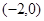 ④
④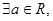 对
对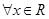 ,使得
,使得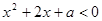 其中真命题为 (填上序号)
其中真命题为 (填上序号)