题目内容
【题目】在一个特定时段内，以点E为中心的7n mile以内海域被设为警戒水域.点E正北55n mile处有一个雷达观测站A，某时刻测得一艘匀速直线行驶的船只位于点A北偏东45°且与点A相距40
n mile的位置B，经过40分钟又测得该船已行驶到点A北偏东
(其中
，
)且与点A相距10
n mile的位置C．
（I）求该船的行驶速度（单位：n mile /h）;
（II）若该船不改变航行方向继续行驶.判断它是否会进入警戒水域，并说明理由.
【答案】（I）船的行驶速度为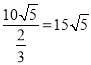
（海里/小时）.（II）船会进入警戒水域.
【解析】
试题(I)根据同角三角函数的基本关系式求出
,然后利用余弦定理求出BC的值，从而可求出船的行驶速度.
(II)判断船是否会进入警戒水域，关键是看点E到直线l的距离与半径7的关系，因而可求出直线l的方程，以及E点坐标，然后再根据点到直线的距离公式得到结论.
（I）如图，AB=40
，AC=10
，
由于
,所以cos
=
由余弦定理得BC=
所以船的行驶速度为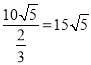（海里/小时）.
（II）解法一 如图所示，以A为原点建立平面直角坐标系，
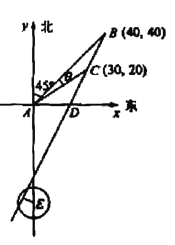
设点B、C的坐标分别是B（x1，y2）, C（x1，y2）,
BC与x轴的交点为D.
由题设有，x1=y1=
AB=40,
x2=ACcos
,
y2=ACsin
所以过点B、C的直线l的斜率k=
,直线l的方程为y=2x-40.
又点E（0，-55）到直线l的距离d=
所以船会进入警戒水域.
解法二: 如图所示，设直线AE与BC的延长线相交于点Q.
在△ABC中，由余弦定理得，
=
=
.
从而
在
中，由正弦定理得，AQ=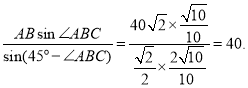
由于AE=55>40=AQ，所以点Q位于点A和点E之间，且QE=AE-AQ=15.
过点E作EP
BC于点P，则EP为点E到直线BC的距离.
在Rt
中，PE=QE·sin
=
所以船会进入警戒水域.
名校课堂系列答案【题目】据统计，某地区植被覆盖面积
公顷
与当地气温下降的度数
之间呈线性相关关系，对应数据如下：
| 20 | 40 | 60 | 80 |
| 3 | 4 | 4 | 5 |
请用最小二乘法求出y关于x的线性回归方程；
根据中所求线性回归方程，如果植被覆盖面积为300公顷，那么下降的气温大约是多少
？
参考公式：线性回归方程
；其中
，
．
【题目】孝感市旅游局为了了解双峰山景点在大众中的熟知度，从年龄在15～65岁的人群中随机抽取n人进行问卷调查，把这n人按年龄分成5组：第一组[15,25)，第二组[25,35)，第三组[35,45)，第四组[45,55)，第五组[55,65]，得到的样本的频率分布直方图如右：
调查问题是“双峰山国家森林公园是几A级旅游景点？”每组中回答正确的人数及回答正确的人数占本组的频率的统计结果如下表.
组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的频率 |
第1组 | [15,25) | 5 | 0.5 |
第2组 | [25,35) | 18 | x |
第3组 | [35,45) | y | 0.9 |
第4组 | [45,55) | 9 | a |
第5组 | [55,65] | 7 | b |
(1)分别求出n，x，y的值；
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人，求第2,3,4组每组各抽取多少人；
(3)在(2)抽取的6人中随机抽取2人，求所抽取的两人来自不同年龄组的概率．
