题目内容
【题目】如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,底面ABCD为菱形,E为棱PB的中点,O为AC与BD的交点,
(Ⅰ)证明:PD∥平面EAC
(Ⅱ)证明:平面EAC⊥平面PBD.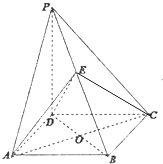
【答案】证明:(Ⅰ)∵ABCD是菱形,O是AC与BD的交点 ∴O是BD的中点;
连接EO.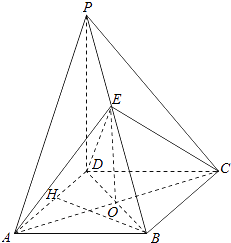
∵E是PB中点,O是BD的中点
∴EO∥PD.
根据直线与平面平行的判定定理可证明:
∴PD∥平面EAC.
(Ⅱ)∵PD⊥平面ABCD,AC平面ABCD,
∴AC⊥PD.∵四边形ABCD是菱形,∴AC⊥BD,
又∵PD∩BD=D,AC⊥平面PBD.
而AC平面EAC,∴平面EAC⊥平面PBD.
【解析】(Ⅰ)由已知得PD∥OE,利用直线与平面平行的判定定理证明即可.(Ⅱ)已知得AC⊥PD,AC⊥BD,由此能证明平面EAC⊥平面PBD.
【考点精析】通过灵活运用直线与平面平行的判定和平面与平面垂直的判定,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一个平面过另一个平面的垂线,则这两个平面垂直即可以解答此题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目