题目内容
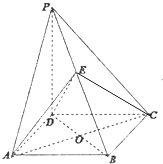
【题目】如图四棱锥E﹣ABCD中,四边形ABCD为平行四边形,△BCE为等边三角形,△ABE是以∠A为直角的等腰直角三角形,且AC=BC. (Ⅰ)证明:平面ABE⊥平面BCE;
(Ⅱ)求二面角A﹣DE﹣C的余弦值.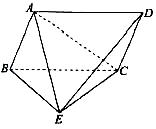
【答案】解:(Ⅰ)证明:设O为BE的中点,连接AO与CO, 则AO⊥BE,CO⊥BE.
设AC=BC=2,则AO=1, ![]() ,AO2+CO2=AC2 ,
,AO2+CO2=AC2 ,
∠AOC=90°,所以AO⊥CO,
故平面ABE⊥平面BCE. 
(Ⅱ)由(Ⅰ)可知AO,BE,CO两两互相垂直.OE的方向为x轴正方向,OE为单位长,
以O为坐标原点,建立如图所示空间直角坐标系O﹣xyz,
则A(0,0,1),E(1,0,0), ![]() ,B(﹣1,0,0),
,B(﹣1,0,0), ![]() ,
,
所以 ![]() ,
, ![]() ,
, ![]() ,
,![]() ,
, ![]() ,
,
设 ![]() =(x,y,z)是平面ADE的法向量,则
=(x,y,z)是平面ADE的法向量,则 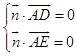 ,即
,即 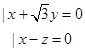 所以
所以 ![]() ,
,
设 ![]() 是平面DEC的法向量,则
是平面DEC的法向量,则 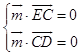 ,同理可取
,同理可取 ![]() ,
,
则 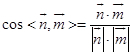 =
= ![]() ,所以二面角A﹣DE﹣C的余弦值为
,所以二面角A﹣DE﹣C的余弦值为 ![]() .
.
【解析】(Ⅰ)设O为BE的中点,连接AO与CO,说明AO⊥BE,CO⊥BE.证明AO⊥CO,然后证明平面ABE⊥平面BCE.(Ⅱ)以O为坐标原点,建立如图所示空间直角坐标系O﹣xyz,求出相关点的坐标,平面ADE的法向量,平面DEC的法向量,利用向量的数量积求解二面角A﹣DE﹣C的余弦值.

练习册系列答案
相关题目
【题目】某公司为了对一种新产品进行合理定价,将该产品按亊先拟定的价格进行试销,得到如下数据:
单价x(元) | 4 | 5 | 6 | 7 | 8 | 9 |
销量V(件) | 90 | 84 | 83 | 80 | 75 | 68 |
由表中数据.求得线性回归方程为 ![]() =﹣4x+a.若在这些样本点中任取一点,則它在回归直线右上方的概率为
=﹣4x+a.若在这些样本点中任取一点,則它在回归直线右上方的概率为
( )
A.![]()
B.![]()
C.![]()
D.![]()