题目内容
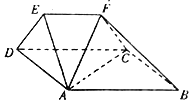
【题目】已知△ABC为等腰直角三角形, ![]() ,
, ![]() ,
, ![]() 分别是边
分别是边![]() 和
和![]() 的中点,现将
的中点,现将![]() 沿
沿![]() 折起,使平面
折起,使平面![]() ,
, ![]() 分别是边
分别是边![]() 和
和![]() 的中点,平面
的中点,平面![]() 与
与![]() ,
, ![]() 分别交于
分别交于![]() ,
, ![]() 两点.
两点.
(1)求证: ![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)求![]() 的长.
的长.
【答案】(1)见解析,(2) ![]() ;(3)
;(3) ![]() .
.
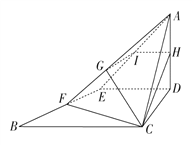
【解析】试题分析:(1)ED∥平面BCH,ED∥HI,又因为ED∥BC,所以IH∥BC;(2)建立空间直角坐标系,n1=(1,-1,1),n2=(0,1,2),求出二面角;(3)![]() =λ
=λ![]() ,由
,由![]() ·n2=0,解得λ=
·n2=0,解得λ=![]() ,所以AG=
,所以AG=![]() AF=
AF=![]()
![]() =
=![]() .
.
试题解析:
(1)证明:因为D,E分别是边AC和AB的中点,所以ED∥BC.
因为BC平面BCH,ED平面BCH,所以ED∥平面BCH.
因为ED平面BCH,ED平面AED,平面BCH∩平面AED=HI,所以ED∥HI.
又因为ED∥BC,所以IH∥BC.
(2)如图,建立空间直角坐标系,由题意得,D(0,0,0),E(2,0,0),A(0,0,2),F(3,1,0),C(0,2,0),H(0,0,1),B(4,2,0),![]() =(-2,0,2),
=(-2,0,2),![]() =(1,1,0),
=(1,1,0),![]() =(0,-2,1),
=(0,-2,1),![]() =
=![]()
![]() =(1,0,0).
=(1,0,0).
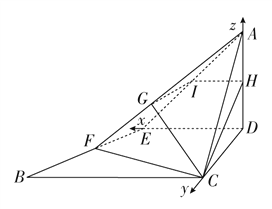
设平面AGI的法向量为n1=(x1,y1,z1),
则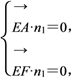
![]()
令z1=1,解得x1=1,y1=-1,则n1=(1,-1,1).
设平面CIG的法向量为n2=(x2,y2,z2),
则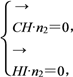
![]()
令z2=2,解得y2=1,则n2=(0,1,2).
所以cos〈n1,n2〉=![]() =
=![]() ,所以二面角A-GI-C的余弦值为
,所以二面角A-GI-C的余弦值为![]() .
.
(3)由(2)知,![]() =(3,1,-2),
=(3,1,-2),
设![]() =λ
=λ![]() =(3λ,λ,-2λ),0<λ<1,
=(3λ,λ,-2λ),0<λ<1,
则![]() =
=![]() -
-![]() =(0,0,-1)-(3λ,λ,-2λ)=(-3λ,-λ,2λ-1),由
=(0,0,-1)-(3λ,λ,-2λ)=(-3λ,-λ,2λ-1),由![]() ·n2=0,解得λ=
·n2=0,解得λ=![]() ,
,
故AG=![]() AF=
AF=![]()
![]() =
=![]() .
.

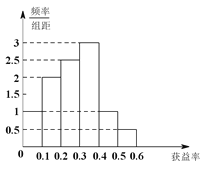
【题目】一网站营销部为统计某市网友2017年12月12日在某网店的网购情况,随机抽查了该市60名网友在该网店的网购金额情况,如表:
网购金额 (单位:千元) | 频数 | 频率 |
| 3 |
|
|
|
|
| 9 |
|
| 15 |
|
| 18 |
|
|
|
|
合计 | 60 |
|
若将当日网购金额不小于2千元的网友称为“网购达人”,网购金额小于2千元的网友称为“网购探者”,已知“网购达人”与“网购探者”人数的比例为![]() .
.
(1)确定![]() ,
,![]() ,
,![]() ,
,![]() 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;

(2)试根据频率分布直方图估算这60名网友当日在该网店网购金额的平均数和中位数;若平均数和中位数至少有一个不低于2千元,则该网店当日评为“皇冠店”,试判断该网店当日能否被评为“皇冠店”.