题目内容
【题目】在直角坐标系![]() 中,椭圆
中,椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
, ![]() 也是抛物线
也是抛物线![]() 的焦点,点
的焦点,点![]() 为
为![]() 与
与![]() 在第一象限的交点,且
在第一象限的交点,且![]() .
.
(1)求![]() 的方程;
的方程;
(2)平面上的点![]() 满足
满足![]() ,直线
,直线![]() ,且与
,且与![]() 交于
交于![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]() ,或
,或![]() .
.
【解析】试题分析:(1)由抛物线定义确定M点坐标,代人椭圆方程,再结合焦点坐标,列方程组解得![]() (2)由
(2)由![]() ,直线
,直线![]() ,得
,得![]() 与
与![]() 的斜率相同,再根据
的斜率相同,再根据![]() ,得
,得![]() .设直线方程
.设直线方程![]() .并与椭圆方程联立,结合韦达定理代人化简可得m值
.并与椭圆方程联立,结合韦达定理代人化简可得m值
试题解析:(1)由![]() 知
知![]() ,
,
设![]() ,
, ![]() 在
在![]() 上,因为
上,因为![]() ,所以
,所以![]() ,
,
得![]() .
.
![]() 在
在![]() 上,且椭圆
上,且椭圆![]() 的半焦距
的半焦距![]() ,于是
,于是
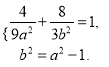 消去
消去![]() 并整理得
并整理得![]() ,
,
解得![]() (
(![]() 不合题意,舍去).
不合题意,舍去).
故椭圆![]() 的方程为
的方程为![]() .
.
(2)由![]() 知四边形
知四边形![]() 是平行四边形,其中心为坐标原点
是平行四边形,其中心为坐标原点![]() .
.
因为![]() ,所以
,所以![]() 与
与![]() 的斜率相同,
的斜率相同,
故![]() 的斜率
的斜率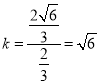 .
.
设![]() 的方程为
的方程为![]() .
.
由 消去
消去![]() 并化简得
并化简得![]() ,
,
设![]() ,
, ![]() .
.
因为![]() ,所以
,所以![]() .
.
![]()
![]()
![]()
![]() .
.
所以![]() .
.
此时![]() ,
,
故所求直线![]() 的方程为
的方程为![]() ,或
,或![]() .
.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目