题目内容
18.已知函数f(x)=ln|x|-x2+ax,其中a∈R.(1)当a=1时,求函数的单调增区间.
(2)l为f(x)在x=x0处的切线,且f(x)图象上的点都不在l的上方,求x0的取值范围.
分析 (1)先求出函数f(x)的定义域,当a=1是求出f(x)的导数,得到极值点,写出单调区间即可.
(2)表示出f(x)在x=x0处的切线,构造新的函数g(x),则由题意知g(x)≤0恒成立,求解即可.
解答 解:(1)定义域为{x|x≠0,x∈R},当x>0⇒$f'(x)=\frac{1}{x}-2x+1$;当x<0⇒
$f'(x)=\frac{1}{x}-2x+1$.故$f'(x)=\frac{1}{x}-2x+1=-\frac{2{x}^{2}-x-1}{x}=0$⇒${x}_{1}=-\frac{1}{2},{x}_{2}=1$,
从而f(x)的单调递增区间为$(-∞,-\frac{1}{2}),(0,1)$.
(2)$f'(x)=\frac{-2{x}^{2}+ax+1}{x}$,l:y=f'(x0)(x-x0)+f(x0)
令g(x)=f(x)-f'(x0)(x-x0)-f(x0),由题意,g(x)≤0恒成立.
g'(x)=f'(x)-f'(x0)=-$\frac{2(x-{x}_{0})(x+\frac{1}{2{x}_{0}})}{x}$
x0>0时:若x>0,则g(x)max=g(x0),若x<0,则$g(x)_{max}=g(-\frac{1}{2{x}_{0}})$
x0<0时:若x>0,则$g(x)_{max}=g(-\frac{1}{2{x}_{0}})$,若x<0,则g(x)max=g(x0)
综上,原条件等价于g(x0)≤0且$g(-\frac{1}{2{x}_{0}})≤0$,易得g(x0)=0符合题意.
故$g(-\frac{1}{2{x}_{0}})≤0$⇒$ln(2{x}_{0}^{2})+{x}_{0}^{2}-\frac{1}{4{x}_{0}^{2}}≥0$.令t=${x}_{0}^{2}$⇒$ln(2t)+t-\frac{1}{4t}≥0$
设h(t)=ln(2t)+t-$\frac{1}{4t}$⇒$h'(t)=\frac{(2t+1)^{2}}{4{t}^{2}}>0$⇒h(t)↑,又$h(\frac{1}{2})=0$
∴$h(t)≥0=g(\frac{1}{2})$?$t≥\frac{1}{2}$⇒${\;}x_{0}∈(-∞,-\frac{\sqrt{2}}{2}]∪[\frac{\sqrt{2}}{2},+∞)$
点评 本题主要考查利用导数求函数的单调区间以及利用导数证明函数小于零或者大于零的问题,属于难题,在高考中作压轴题出现.

| A. | a>b>c | B. | a>c>b | C. | b>c>a | D. | c>b>a |
| A. | $\frac{{x}^{2}}{84}$-$\frac{{y}^{2}}{16}$=1 | B. | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{84}$=1 | ||
| C. | $\frac{{x}^{2}}{100}$-$\frac{{y}^{2}}{84}$=1 | D. | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{84}$=1或$\frac{{x}^{2}}{100}$-$\frac{{y}^{2}}{84}$=1 |
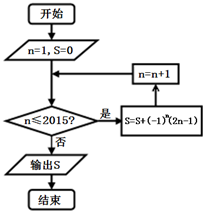
| A. | 2015 | B. | 2016 | C. | -2015 | D. | -2016 |
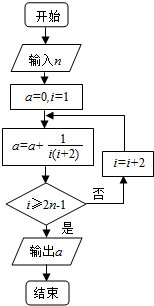
| A. | $\frac{2015}{4031}$ | B. | $\frac{4030}{4031}$ | C. | $\frac{2014}{4029}$ | D. | $\frac{2015}{4029}$ |
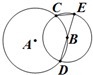 如图,圆A与圆B交于C、D两点,圆心B在圆A上,DE为圆B的直径.已知CE=1,DE=4,则圆A的半径为4.
如图,圆A与圆B交于C、D两点,圆心B在圆A上,DE为圆B的直径.已知CE=1,DE=4,则圆A的半径为4.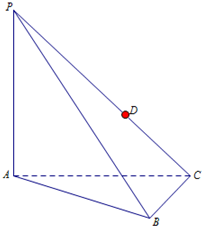 如图,在三棱锥P-ABC中,△ABC为等边三角形,AB=2,AP⊥平面ABC,D为PC上的动点.
如图,在三棱锥P-ABC中,△ABC为等边三角形,AB=2,AP⊥平面ABC,D为PC上的动点.